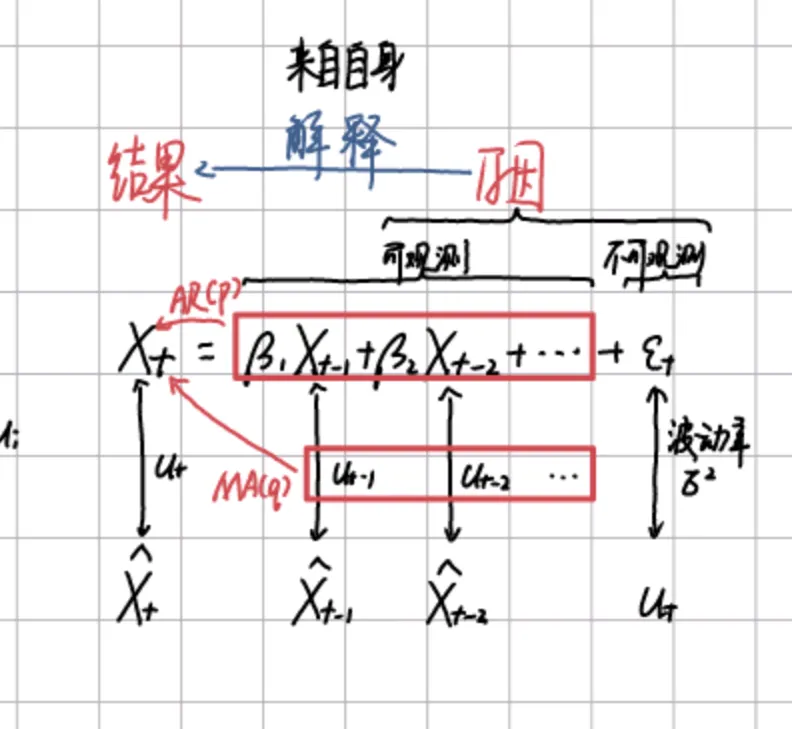
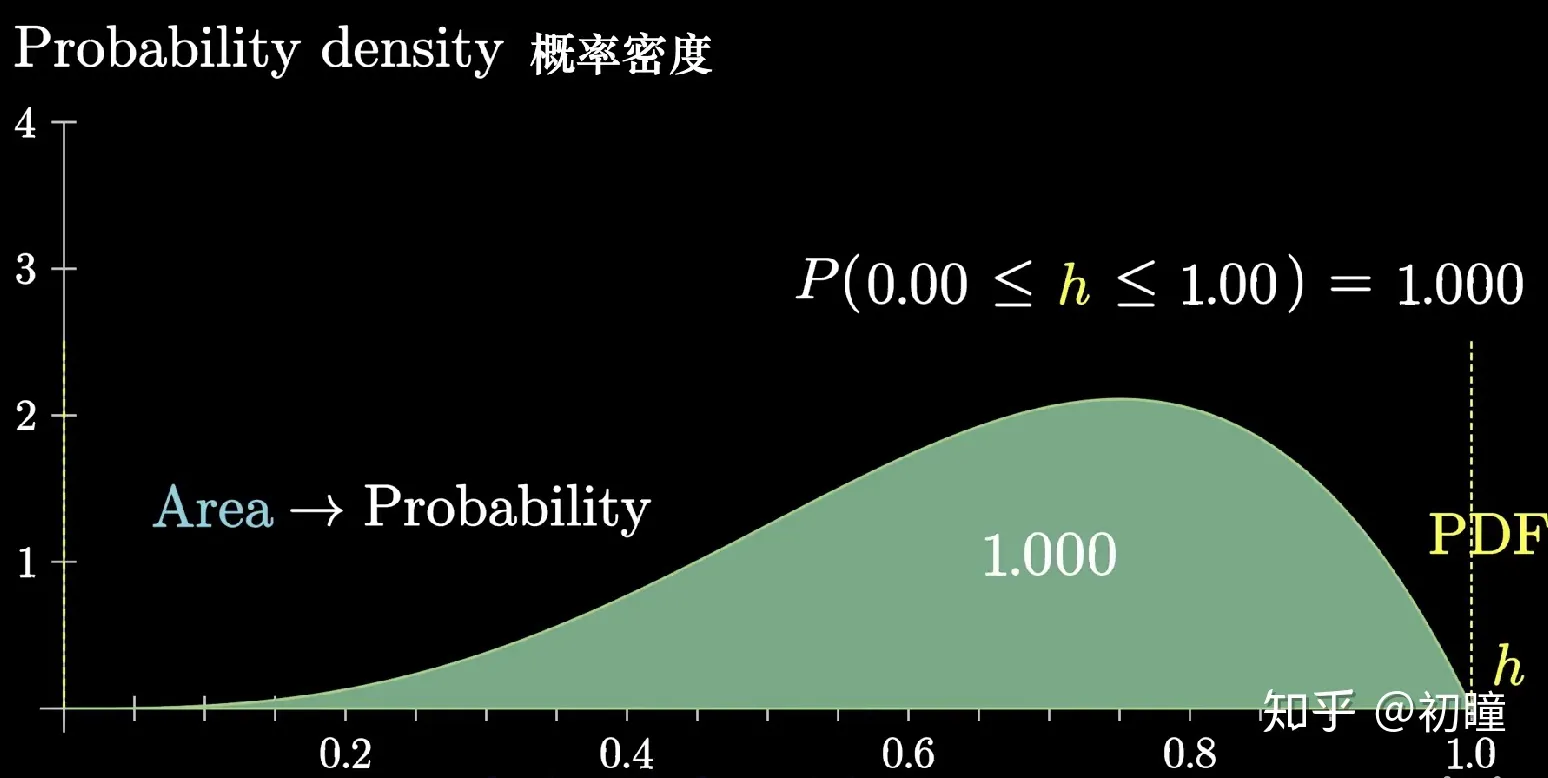
在这一章中，我们考虑 变量 出现特殊情况时的研究。

滞后变量

在过往章节中，我们都认为变量是随机的。但考虑现实情况，以下两种变量存在特殊情况：

  • 滞后变量
    某一期的数据会对今后多期数据产生“深远影响”。
    • 如果只是解释变量存在滞后，我们就称之为 分布滞后模型；
    • 如果只是被解释变量存在滞后，我们就称之为 自回归模型

分布滞后

根据滞后的不同特点（过去经验对未来数据的影响程度），我们一般分为：

  • 递减滞后
  • 不变滞后
  • 倒 ∧\land 形

核心假设
一件事情能带来的影响是基于事情本身的，滞后变量的取值来源于原始数据，再根据经验乘上对应结构的权数，有

滞后数据=原始数据×权数滞后数据=原始数据\times 权数

把多个滞后变量合成一个新的变量 ZtZ_t，回归方程就是

Yt=α0+β0Zt+μtY_t=\alpha_0+\beta_0 Z_t +\mu_t

这个方法就是 经验加权估计法

为了增加说服力，我们可以选不同的滞后结构多加权几次，选R2R^2、FF 值、tt 值 、DWDW 值最佳的那一种。

但是存在以下问题：

  • XtX_t、Xt−pX_t-p 存在严重多重共线性
  • 滞后长度难以确定
  • 一期一期地增加，观察AIC SIC 值选最优的。

自回归模型

对于无限分布滞后模型

Yt=α+β0Xt+β1Xt−1+⋯+βiXt−i+μtY_t=\alpha+\beta_0 X_t + \beta_1 X_{t-1} + \cdots + \beta_i X_{t-i} + \mu_t

如果滞后长度无法确定，而自身无限滞后，难以进行估计。我们提出自回归模型（转化为一阶自回归模型）

*$$Y_t=\alpha^*+\beta_0^X_t+\beta_t^Y_{t-1}+u_t^$$

库伊克模型

滞后系数的衰减是 λ<1\lambda<1 的等比数列，（几何级数）

不带入具体数据，只做待估参数，βi=β0λi\beta_i=\beta_0\lambda^i，原式变为

Yt=α+β0∑t=0∞λiXt−i+μtY_t=\alpha +\beta_0\sum_{t=0}^{\infin}\lambda^i X_{t-i}+\mu_t

取滞后一期

Yt−1=α+β0∑t=1∞λi−1Xt−i+μt−1Y_{t-1}=\alpha +\beta_0\sum_{t=1}^{\infin}\lambda^{i-1} X_{t-i}+\mu_{t-1}

然后等号两端同乘以 λ\lambda ，利用错位相减法可得出

Yt−λYt−1=(1−λ)α+β0Xt+(μt−λut−1)Y_t-\lambda Y_{t-1}=(1-\lambda)\alpha+\beta_0 X_t + (\mu_t-\lambda u_{t-1})

即

Yt=(1−λ)α+β0Xt+λYt−1+(μt−λut−1)Y_t=(1-\lambda)\alpha + \beta_0 X_t+ \lambda Y_{t-1} + (\mu_t-\lambda u_{t-1})

进一步，令α∗=(1−λ)α\alpha^*=(1-\lambda)\alpha，β0∗=β\beta_0^*=\beta，β1∗=λ\beta_1^*=\lambda，μt∗=μt−λμt−1\mu_t^* =\mu_t- \lambda\mu_{t-1}可转换为一阶自回归

Yt=α∗+β0∗Xt+βt∗Yt−1+ut∗Y_t=\alpha^*+\beta_0^*X_t+\beta_t^*Y_{t-1}+u_t^*

自适应预期模型

Yt=α+βXt∗+utY_t=\alpha+\beta X_t^*+u_t

  • X的预期影响Y的现状
  • 自适应预期假设，然后做一阶差分

局部调整模型

Y的预期影响X的现状，因为X事件的变化而调整对Y的预期从而适应X的新现状，例如超市纸巾促销，由于价格X的降低，影响人们对购买量Y的预期，从而适应低价的X的现状


实际变化是预期的一部分

问题

虚拟变量

表示对象的属性、特征，定性的赋值给虚拟变量D

例如：有没有？

  • 有，赋值 D=1D=1，比较类型
  • 没有，赋值 D=0D=0，基础类型

每提一个问题，就引入一个D。一个问题有m个选项，就提m-1次问

引入方式

作为解释变量

  • 加法引入 改变截距 [+β1Di][+\beta_1 D_i]
  • 乘法引入 改变斜率 [][]
    • 回归模型比较
    • 交互效应分析
    • 分段线性回归

作为被解释变量，变为二项选择模型