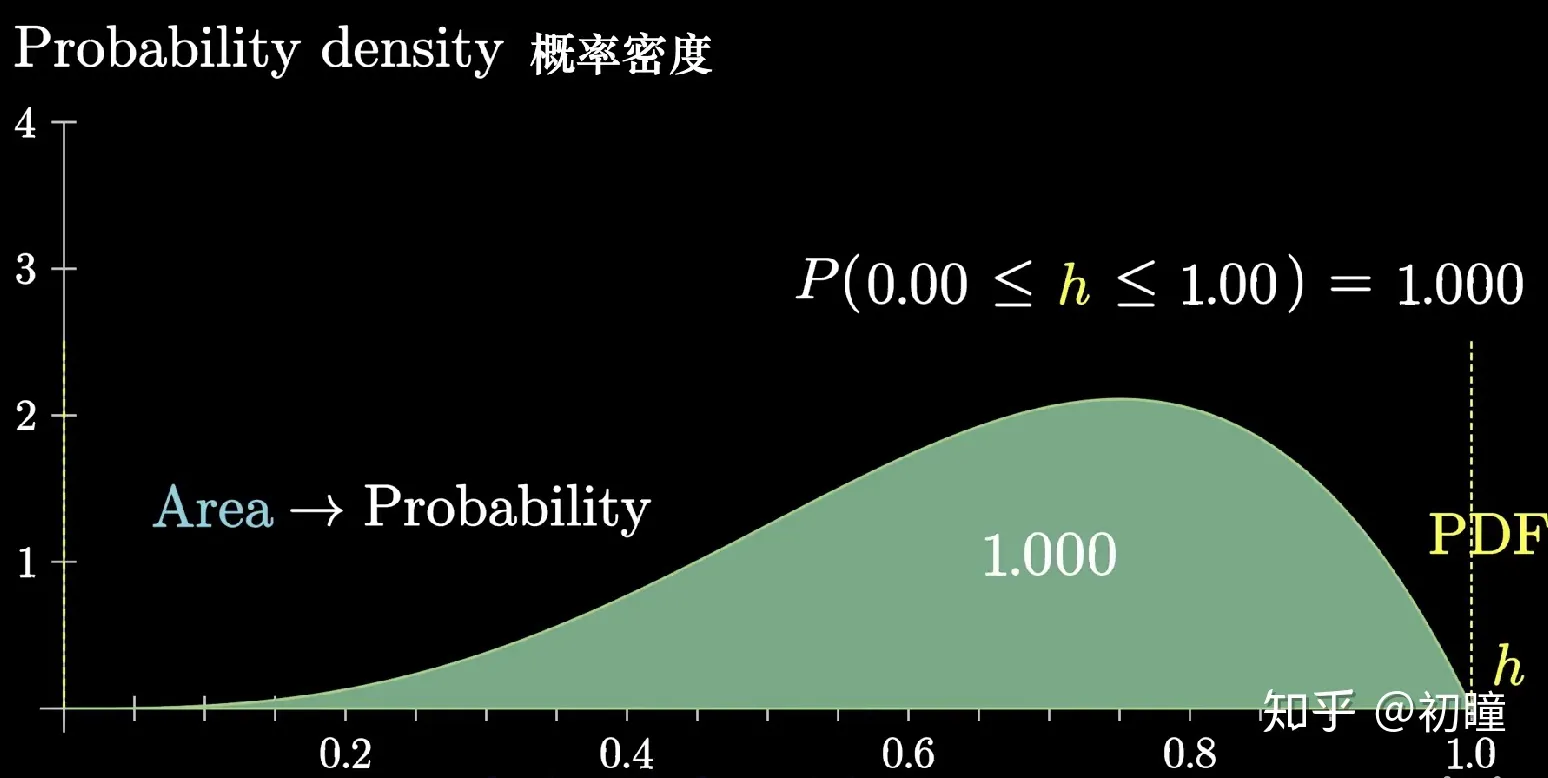
没有数学的帮助,今天的金融理论都将失去生存的根基。

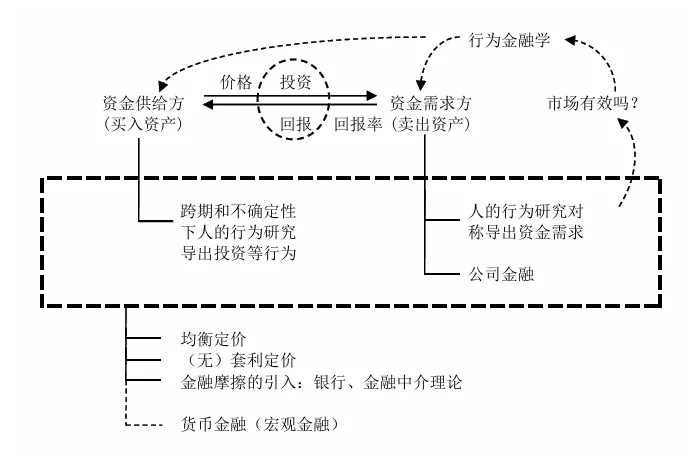
金融是指资金的融通,是资产和负债随时间的推移在确定以及不确定性状态下分配的动态过程。
maxu(C0)+δE[u(cs)]
消费者跨期效用最大化的求解
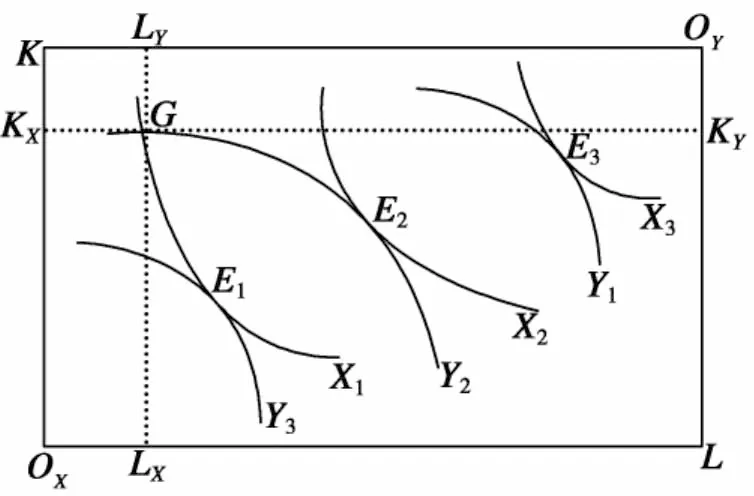
站在投资者的角度,如何精确地给资产定价、计算收益率,是投资是否有利可图的重要依据。借助数学,经济学发展出两条路径:一条路径从最基础的资源禀赋、投资者偏好出发,思考市场的供给与需求,通过建立一般均衡,建立整个经济体的数学模型,资产定价问题便转化为了求解均衡问题,从而有迹可循。

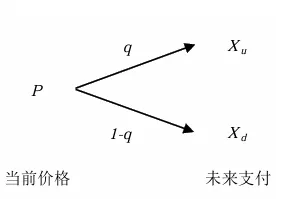
另一条路径从套利问题出发,在无套利机会的假设下通过复制资产,构建资产价格变化的二叉树,把资产的价格变化问题转化至二叉树生成的空间中,价格的求解就是对二叉树定价方程的求解。


C0=e−r(u−der−dCu+u−du−erCd)=e−rEQ[c~]
单期二叉树模型下衍生品价格的定价方程
二叉树步数趋于无限时,定价问题就收敛至B-S公式,通过求解偏微分方程来探索资产定价的内涵。
∂t∂f+rSt∂S∂f+21σ2St2∂S2∂2f=rf
衍生品定价的Black-Scholes偏微分方程
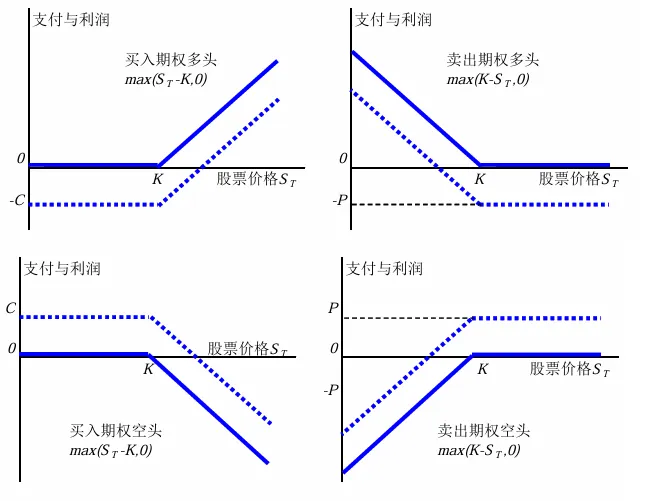
 欧式期权的支付情况
欧式期权的支付情况
无套利思想成熟后,第二条路径实际上就把资产定价问题转化为在某个概率测度下求数学期望的问题。例如期权等金融衍生品,其价格变化与其标的资产紧密相关,而其收益率在连续时间上是一个几何布朗运动,期权价格的求解就是对此几何布朗运动进行分析,人们会惊奇的发现,数百年前源自对花粉无规律运动的分析求解,实际上成为了今天蓬勃发展的金融市场的重要内驱力。
C0=S0N(b−σTlnK−LnS0−(r−21σ2)T)+e−rTKN(−σTlnK−LnS0−(r−21σ2)T)
欧式买入期权的Black-Scholes公式
得出了资产价格的求解方法后,人们会从更大的角度思考市场是否有效的问题。实证经济学家利用最小二乘法作为他们有力的工具,如CAPM、Fama三因子模型等通过利用拟合方程,估计出收益率变动的显示路径,市场弱势有效的问题也就转化为是否为随机游走的分析。
r~0−rf=α0+n=1∑Nβ0,nr~n+ε0~
收益率的多因子模型
而当我们再次将眼光放回投资者身上,我们会注意到人的行为同样不可忽视。作为资金的供给、需求者,企业的投资、融资、分红决策和行为、资本结构等问题,以及自身的经营状况,都需要借助数学制作财务报表,从而政府、股东等利益相关可以知道公司经营的状况,投资者可以做出投资决策、企业估值等分析。
S0=t∑∞(1+r)tDt=t∑∞(1+r)tD1(1+g)t−1=r−gD1
戈登股利增长模型
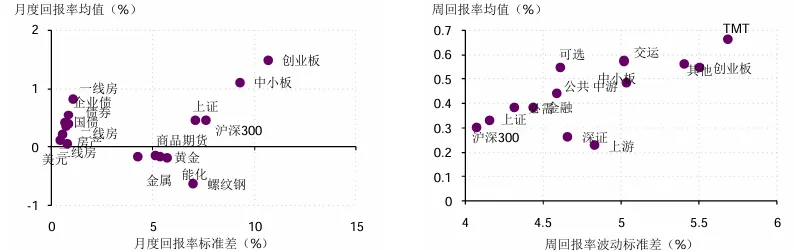
 中国各行业、板块的均值方差图
中国各行业、板块的均值方差图
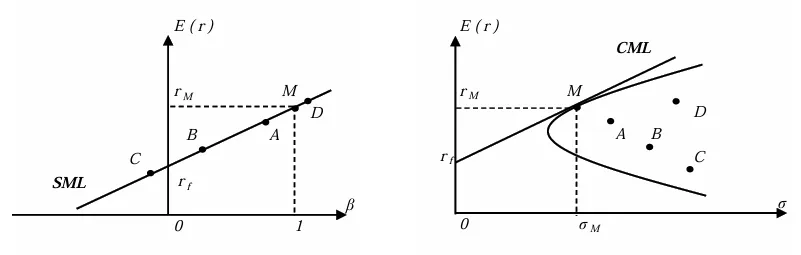
 资本市场线与证券市场线
资本市场线与证券市场线
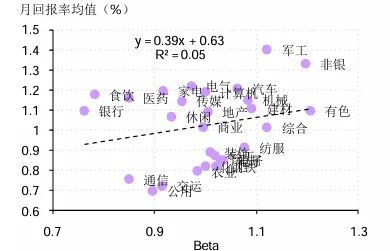
 用中国股票市场数据估算的证券市场线
用中国股票市场数据估算的证券市场线
 多因子模型用于股票投资决策
多因子模型用于股票投资决策
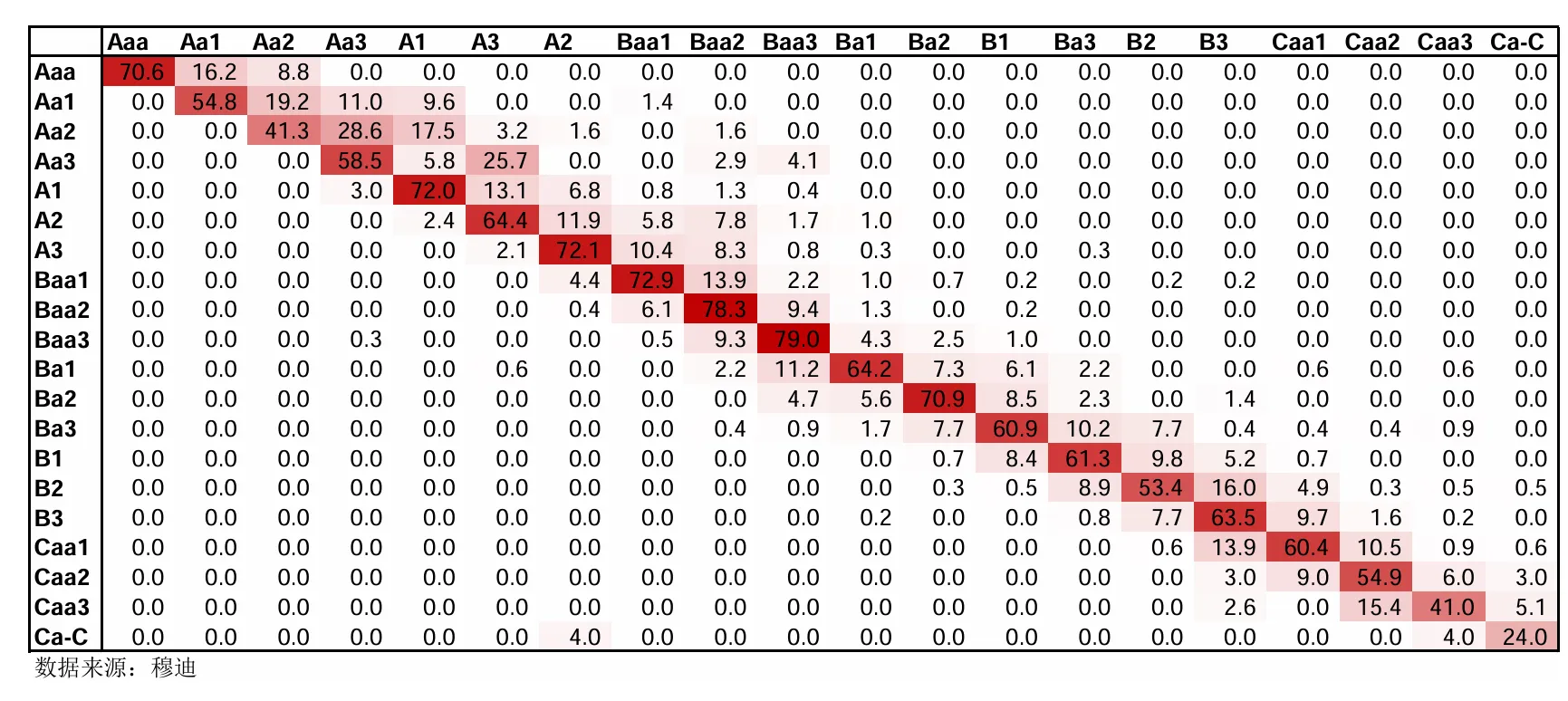
 全球评级迁徙率:2012-2013年(单位%)
全球评级迁徙率:2012-2013年(单位%)
目光回到整个金融体系中,其中的中介如商业银行、保险公司、投资银行等金融机构,以及作为政府参与市场的重要媒介的中央银行,让我们对于金融的理解加以外延:货币的发行、流通、回笼,贷款的发放与收回,存款的存入与提取,汇兑的往来等经济活动,这就形成了宏观金融。和研究资产定价问题的微观金融一样,金融的大厦正是借助一个又一个数学模型不断向上搭建,构建出了如今的金融世界。
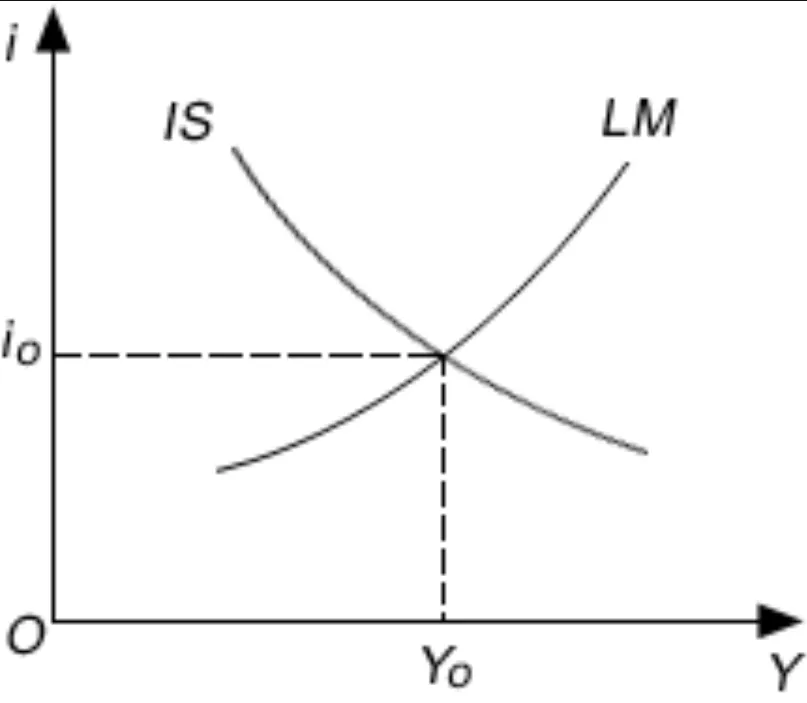
 IS-LM模型
IS-LM模型