引言

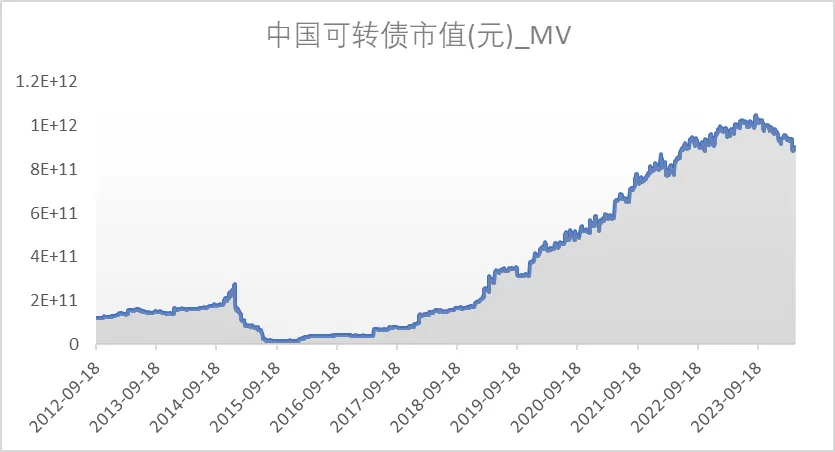
在我国经济步入新时代并逐渐与国际金融体系接轨的背景下，我国金融市场展现出多样化的发展态势。其中，可转债市场作为金融市场的重要组成部分，近年来实现了快速增长。特别是自2017年9月可转债申购方式从价格申购转变为信用申购以来，上市公司通过可转债融资的规模呈现爆炸性增长，2017年的发行规模便突破了900亿元人民币，较2016年增长了超过四倍。2019年至2022年间，融资规模更是连续突破2000亿元大关，可转债已成为上市公司主要的融资工具之一。尽管如此，市场上仍存在大股东利用可转债进行短线操作以谋取利益的现象，这暴露了市场效率的问题。为此，中国证监会于2020年颁布了《可转换公司债券管理办法》，旨在通过强化顶层设计、完善交易机制和投资者适当性制度等措施，来抑制可转债交易风险并加强投资者保护。2022年6月17日，上交所和深交所进一步发布了关于限制可转债涨跌幅和提高交易门槛的通知。鉴于此，对我国可转债市场的有效性进行实证研究具有重要的现实意义。本研究选取2002年12月31日至2024年4月30日期间的中证可转换债券指数（000832）作为样本，对我国可转债市场的弱势有效性进行了深入分析。

文献综述

在中国学术界，市场有效性的研究主要采用实证方法，检验证券市场的有效性。大多数研究集中在沪深股票市场，而对可转债市场的有效性研究相对较少。

可转换债券是一种特殊的公司债券, 又称为可转股、可兑股债或可转称公司债券。转换债券是一种混合债券,它既包含了普通债的特征,也包含了权益特征,同时,它还具有相应于标的股票的衍生特性。它包含着很多的期权。这些期权主要有:投资者按照一定价格在一定期限内将债券转换成公司股票的期权( 转股权) ,投资者在一定条件下将债券按照一定价格回售给公司的期权( 回售权) , 公司在一定条件下调整转股价格的期权( 转股价格调低权) ,以及公司在一定条件下赎回可转债的期权( 赎回权)。对于标准的可转换债券,在价值形态上,可转换债券赋予投资人一个保底收入,即由债券息票支付与到期本金偿还构成的普通付息债券的价值,同时,它还赋予了投资人在股票上涨到一定的条件下转换成发行人普通股票的权益, 即看涨期权的价值。对于发行人而言,为了实现在公司股价上涨或者市场环境发生变化的情况下低成本融资, 发行人可在一定的条件下行使赎回权力,即发行人提前赎回的期权。可转换债券既能给投资者一确定的现金流,锁住风险,又能提供公司股价上涨所产生的投资获利机会。兼具筹资和避险的双重功能。从国际市场上来看,它成为众多发达国家金融资产的主要组成部分。

Paul Samuelson在1965年提出有效市场假说（EMH），认为在信息流畅的市场上，价格变化不可预测，因为它们反映了市场参与者的期望和现有信息。Fama对EMH进行了系统总结，提出了一个完整的理论框架。他和Robert将有效市场分为弱式、半强式和强式三种假设。在弱式有效市场中，证券价格反映了所有可获得的历史信息；在半强式有效市场中，证券价格反映了所有可 获得的历史和当前的公开信息；在强式有效市场中，证券价格不仅反映了所有历史信息和当前的公开信息， 而且能够反映投资者的私有信息。有效市场的价格走势通常通过“随机游走”（Random Walk）或“鞅过程”（Martingale）来描述，其核心逻辑是，如果价格能够反映当前证券的所有信息，那么证券价格变动仅反映了与当前价格水平无关的未来新信息的变化；由于未来信息流的变化无法预测，因此价格的变化也无法被预测。由于证券当前的所有信息都被包含在价格之中，因而基于过去证券历史价格信息预测未来价格的技术分析，以及基于公司 历史盈利状况分析和挑选低估值证券的基本面分析将统统失效。

本文梳理了中国学者对证券市场弱势有效性的研究，发现存在两种观点：

一些学者认为中国股票市场已达到弱势有效性。例如，杨朝军（2000）利用秩相关系数得出结论，1993年后中国股票市场达到弱式有效。宋颂兴（1995）通过游程检验和序列相关检验得出沪市已达到弱式有效。文德才（1999）运用正态分布检验、序列相关检验、非参数检验后得出结论，我国股市具有弱式有效。张光国（1999）运用游程检验法、累计超常收益分析法实证后得出结论，深市已达到弱式有效。杨朝军（1997）运用K-S检验、序列自相关检验得出结论，我国股票市场自1993年以来已趋于弱式有效。陈小悦（1997）运用随机游走模型、ADP检验得出结论，沪市自1993年后达到弱式有效，而深市已达到弱式有效。陈立新（2002）冉茂盛（2001）李晓静（2006）等学者采用不同的指数和方法对我国股票市场有效性进行检验，结果发现中国股票市场显示一定的弱式有效性。

另一些学者则认为中国股票市场未达到弱势有效性。瞿慧、刘烨、李娟（2011）基于遗传编程的股票指数技术交易系统进行分析得出结论，我国股票市场尚未达到弱式有效。谢德辉、董俊（2011）建立了股票市场供需均衡、市场出清的分析框架分析得出结论，我国股票市场短期不是有效市场，存在套利和获取超额收益的机会。俞乔（1994）对我国股票市场进行误差项序列相关检验、游程检验、非参量性检验后得出结论，沪、深股市不具有弱式有效性。魏玉根（2002）进行市场TTS模拟、符合检验法检验证明我国股市不具备真正的弱式有效。张亦春（2001）运用广义谱域分析法也得出结论，目前我国股市还不真正具备弱式有效。解保华，高荣兴（2002）、李兴绪，郑树明（2004）、谢晓霞（2007）等分别运用不同的实证分析方法，如单位根、方差比（VR）和Q统计量自相关检验和游程检验等论证了我国股票市场并未达到弱势有效。

我国可转换债券市场弱式有效性的研究目前处于起步阶段，研究的学者和文献相对较少。主要结论有：黄建兵（2002）用纯套利检验对我国可转换债券市场进行了实证得出结论，可转债市场目前存在套利机会，但这种机会正在不断减少。也就是我国可转换债券市场未达到弱势有效性。张信东（2005）采用时间序列自相关检验法进行实证分析得出结论，目前我国可转债市场尚未达到弱式有效。郑振龙和康朝锋（2005）采用反例形式运用绝对占优思想得出结论，我国可转换债券市场效能不足。

通常，学者利用随机游走理论来检验证券市场是否弱式有效。因为证券价格变化是否遵循随机漫步形式可以检验证券价格对信息流动的反应。随机游走理论假设，如果证券市场价格是随机的，那么从该市场获得的收益是不可测且随机的，所以我们可以假设市场是有效的。因此，一个达到弱有效的可转债市场应当符合“随机游走理论”，对于可转债市场弱势有效性的检验就在于对数据随机性的检验。

实证分析

在检验可转债市场的弱势有效性时，我们考虑可转债的时间序列是否程序随机状态，即价格之间无自相关性。本文首先对时间序列数据进行平稳性的单位根检验，如果是非平稳的，则需进一步检验价格的序列相关性，若不相关则认为价格服从随机游走，我国可转债市场达到弱势有效。同时，本文还利用游程检验、Hurst指数的计算等方法，从多角度对可转债市场的弱势有效性进行检验。

数据和描述性统计

中证可转债及可交换债券指数样本券由沪深交易所上市的可转换公司债券和可交换公司债券组成。指数采用市值加权计算，以反映沪深交易所可转换公司债券和可交换公司债券的整体表现。本文选取了选取2002年12月31日至2024年4月30日中证可转换债券指数（000832） 的5179个日数据进行检验。为消除可能存在的异方差，对中证可转换债券指数进行对数差分，并计算对数收益率。数据来源为锐思数据库。报告期指数的计算公式为

$$报告期指数=\frac{报告期样本债券总市值}{除数}\times 100$$

其中，$报告期样本债券总市值= \sum (全价\times 发行量)$，$全价=净价+应计利息$​​​。

对数收益率的计算公式为：

$$R_t=\ln{\frac{P_t}{P_{t-1}}}$$

其中，$P_t$为当期价格，$P_{t-1}$为前一期价格。

我们对十二年间的可转债指数变化趋势进行分析，发现我国可转债指数呈现出较强的时间趋势。

实证检验

单位根检验

本研究选取2002年12月31日至2024年4月30日期间的中证可转换债券指数（000832）作为样本，利用Stata对中证可转换债券指数及其对数差分得到的收益率进行ADF单位根检验，结果如下表：

MacKinnon approximate p-value for Z(t)_p = 0.0799
MacKinnon approximate p-value for Z(t)_r = 0.0000

由上表可以看出，指数价格序列的ADF值均大于在1%、5%的临界值，但小于10%水平下的临界值，说明可转债指数价格在1%、5%的置信水平下，是不平稳的，存在单位根，在10%的置信水平下是平稳的，无单位根。收益率序列的ADF值均小于各自在1%、5%、 10%水平下的临界值，收益率序列在1%、5%、10%置信水平下都是平稳的无单位根，这说明经过一阶对数差分后，数据具有平稳性，不存在单位根。价格序列对应的p=0.0799>0.05，说明价格序列不平稳；收益率序列对应的p=0.0000，收益率序列是平稳的。

序列相关性检验

由于价格时间序列数据是非平稳的，所以要对价格序列进行相关性检验。假设可转债市场是弱势有效的，那么价格指数就是一个随机游走序列，其波动应满足一个随机过程，首先建立序列相关检验的自回归模型：

$$P_t=\theta_0+\theta_iP_{t-1}+\varepsilon_t$$

$P_t$代表可转债指数价格，$\theta_i$为第t期与第t-i期的自相关系数，$\varepsilon_t$为随机误差项，表示实际价格与期望价格的差额。如果随机游走过程成立，$\varepsilon_t$​ 作为价格变动的误差项，不应该存在序列相关性。因此可以运用Q统计量判断残差项是否存在自相关。在stata软件中，计算自相关和偏自相关系数，结果如下：

可以看出，p具有很强的自相关性，而r也具有较强的自相关性。进一步，计算p和r的Q统计量结果如下：

Portmanteau test for white noise	p	r
Portmanteau (Q) statistic	88625.3923	350.6605
Prob>chi2(40)	0	0

由上表的自相关检验结果可 以看出，p、r在样本区间内残差项的一阶自相关系数并显著异于0，而其相应的Q统计量的值在给出的5%的显著性水平下大于临界值。所以可以认为，可转债指数价格、收益率指数都存在序列相关性，价格序列不是随机的，未表现出弱势有效的特征。

游程检验

游程检验是对某个变量出现的取值是否游走进行的检验。对弱式有效市场的检验可以采取随机游走假设检验的思路，如果实证结论支持随机游走的假设，则认为市场弱式有效成立。游程检验的基本假设是：设游程检验的原假设为H0：数据随机，市场为弱式有效；备择假设为H1：数据不随机，市场不是弱式有效。判断标准（利用P值进行判断）。本文将利用Stata软件进行游程检验，在Stata随机性检验中利用游程构造统计量Z，其中 $Z=\frac{R-E(R)}{\sqrt{D(R)}}$（R为游程的个数），并根据正态分布给出相应的概率值。 如果在5%的显著水平下，如果$|\frac{R-E(R)}{\sqrt{D(R)}}|\ge 1.96$，则可以拒绝样本是随机的原假设；如果在5%的显著水平下，如果$|\frac{R-E(R)}{\sqrt{D(R)}}|\le 1.96$，则可以接受样本是随机的原假设。 从P值来看，如果P概率小于或等于显著水平0.05，则拒绝原假设H0 ；如果P概率大于显著性水平0.05，则不能拒绝原假设H0 。

runtest	p	r
N(r<=.0002141896370702)	2590	2589
N(r>.0002141896370702)	2589	2589
obs	5179	5178
N(runs)	88	2222
z	69.55	10.23
Prob>|z|	0.089	0.00

对于价格序列，从Z值来看，其绝对值大于1.96，拒绝原假设，数据不是随机的；从p值来看，大于0.05，因此同样拒绝原假设，沪深可转债市场不是弱势有效的。

Hurst指数检验

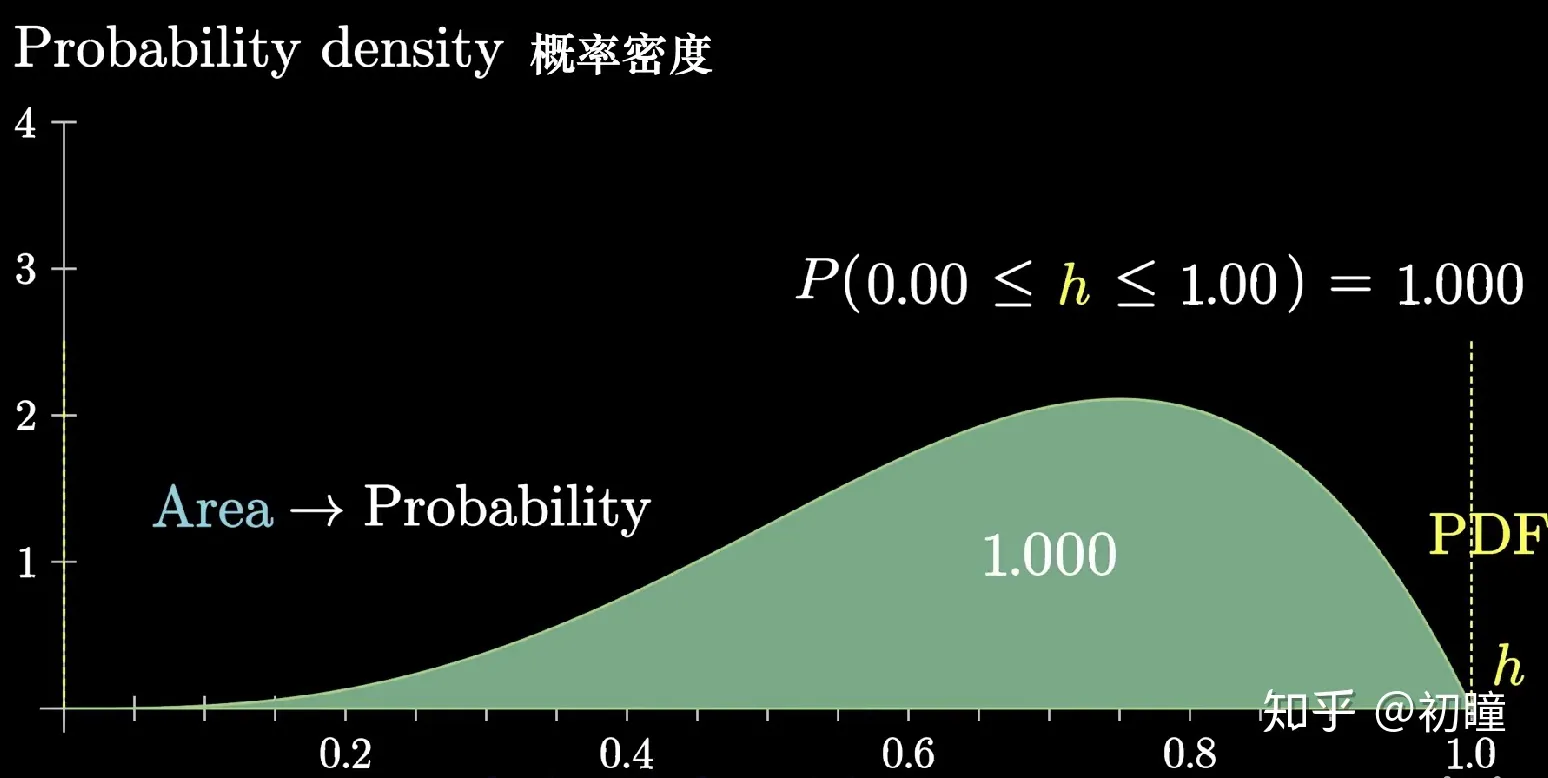
Hurst指数是作为判断时间序列数据遵从随机游走还是有偏的随机游走过程的指标。Hurst指数反映了时间序列长期记忆性的程度，即过去的信息对未来的影响程度。Hurst指数的取值范围为0到1之间，当Hurst指数等于0.5时，时间序列被认为是一种随机漫步，即具有随机性；当Hurst指数大于0.5时，时间序列显示出长期正相关性，表明趋势在未来可能持续；当Hurst指数小于0.5时，时间序列显示出长期负相关性，表明趋势在未来可能反转。Hurst的计算方法如下：

对于时间序列x，将数据分割为长度为r的g组互不重叠的子序列，对每一组子序列进行下列计算：

• 计算均值$\bar{x_i}=\frac{1}{r}\sum_{j=1}^{r}x_{ij}$
• 计算离差$y_{ij}=x_{ij}-\bar{x_i}$
• 计算累计离差$z_{ij}=\sum_{k=1}^{j}y_{ik}$
• 计算极差$R_i=max(z_{ij})-minz(_{ij})$
• 计算标准差$s_i=\sqrt{\frac{1}{r-1}\sum_{j=1}^{r}(x_{ij}-\bar{x_i})^2}$
• 计算RS值$RS_i=\frac{R_i}{S_i}$​

对计算出来的各个子序列的RS值求平均，得到

$$\bar{RS}=\frac{1}{g}\sum_{i=1}^{g}(RS_i-\bar{RS})^2$$

并求其标准差，得到

$$S_{RS}=\sqrt{\frac{1}{g-1}\sum_{i=1}^{g}(RS_i-\bar{RS})^2}$$

使用python编程计算得出，p的Hurst指数=0.7487，表明p不是随机的，同样证明沪深可转债市场不存在弱势有效性。

结论

利用中证可转债指数进行单位根检验、序列自相关检验、游程检验、Hurst指数检验，本文得出结论，我国可转债市场不处于弱势有效，这说明投资者很难通过对历史数据的分析获得超额收益。因此，我们应当进一步完善信息披露机制，提高监管能力，注重利用公司基本面信息获利的能力，以此促进我国可转债市场尽快走向弱势有效，促进我国经济快速发展。

参考文献

[1]黄建兵.中国的可转换债券与市场价格有效性研究[J].系统工程理论方法应用,2002(01):63-67.

[2]王梦贤.基于GARCH模型的可转换债定价方法研究[J].沿海企业与科技,2008,(05):18-20.

[3]吕喆.我国可转债市场弱势有效性探讨——基于随机游走理论的可转债指数实证研究[J].商业时代,2012,(26):64-65.

[4]刘云.我国股票市场有效性的实证研究[J].经济界,2015,(01):17-19.

[5]潘征文.中国股票市场有效性研究评述[J].现代经济信息,2011,(21):195-196.

[6]张政.浅析可转债新规对市场的影响[J].债券,2022(11):78-80.

[7]张秀艳,张敏.可转换债券市场与股票市场的波动关系——基于二元GARCH模型的实证研究[J].吉林大学社会科学学报,2009,49(04):133-140.

[8]张秀艳,张敏,闵丹.我国可转换债券市场与股票市场动态传导关系实证研究[J].当代经济研究,2009(08):52-55.

[9]宋芳秀,胡司盾.我国可转债转股的影响因素研究——基于发展阶段和理性程度的分析[J].经济纵横,2021(11):111-120.

[10]贺行知.上海股票市场有效性假说研究[J].投资与创业,2021,32(20):79-82.

[11]姜圆.现代资产定价理论的研究和发展——基于有效市场假说和资产定价模型的视角[J].现代管理科学,2021(03):42-48.

附录

使用代码

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18

tsset date graph twoway line p date, title("中证可转债指数价格走势")ytitle("原数据") xtitle("时间") graph twoway line r date, title("中证可转债指数收益率走势")ytitle("收益率") xtitle("时间") logout, save(基本统计描述) word replace: tabstat p r, s(N mean p50 sd min max skewness kurtosis) format(%12.3f) columns(s) dfuller p dfuller r ac p ac r wntestq p wntestq r runtest p runtest r

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29

# hurst指数计算 import numpy as np import math def hurst_rs(data:list): """ 使用rs法计算Hurst指数值 """ t_i = [] for r in range(2, (len(data))//2 + 1): g = len(data)//r x_i_j = [data[i * r : (i+1)*r] for i in range(g)] x_i_mean = [sum(x_i)/r for x_i in x_i_j] y_i_j = [[x_i_j[i][j] - x_i_mean[i] for j in range(r)] for i in range(g)] z_i_j = [[sum(y_i_j[i][ : j + 1]) for j in range(r)] for i in range(g)] r_i = [max(z_i_j[i])-min(z_i_j[i]) for i in range(g)] s_i = [math.sqrt(sum([ (x_i_j[i][j]-x_i_mean[i])**2 for j in range(r)]) / (r-1)) for i in range(g)] rs_i = [r_i[i]/s_i[i] for i in range(g)] rs_mean = sum(rs_i)/g # t_i.append( math.sqrt(sum([(rs_i[i] - rs_mean)**2 for i in range(g)])/(g-1)) ) t_i.append(rs_mean) return np.polyfit(np.log(np.arange(2, len(data)//2 + 1)), np.log(np.array(t_i)), 1)[0] if __name__ == "__main__": # 测试 data_test = list(np.arange(0, 100)) print(hurst_rs(data_test))

资料整理