高利贷帝国主义是美国资本主义的没落吗？基于ARCH模型的美国联邦基金利率走向分析

张茂源，921107810238

南京理工大学经济管理学院金融1班

摘　要：

本文旨在利用行业的生命周期理论和ARCH模型来分析预测美国联邦基金利率的变化率，从而判断美国资本主义的发展阶段和未来趋势。本文首先综合分析了资本主义的生命周期阶段的划分、特征和美联储联邦基金利率变动周期与经济衰退现象的关系，指出美国资本主义已经进入了衰退期。然后，使用1954年7月1日至2023年11月的联邦基金利率月度收益率的数据，建立了ARCH(2)自回归条件异方差模型，对联邦基金利率的变化率进行动态预测，发现美国加息的趋势不会继续加强，而是会逐渐减弱，最终可能会进入降息周期，同历史周期一致，有经济衰退期现象伴随出现。这一结果与生命周期理论的判断相一致。本文的意义在于：将ARCH模型应用于联邦基金利率的变化率的分析预测，以及将资本主义的发展类比为行业的生命周期，从两个不同的角度、不同维度的理论、实证分析的结合，来对美国资本主义的发展展开更加准确的分析，从而更好地把握资本主义的发展规律。

关键词：

ARCH模型；生命周期理论；经济衰退；美国联邦基金利率；加息；

Is Usury Imperialism the Decline of American Capitalism? An Analysis of the Trend of the Federal Funds Rate Based on the ARCH Model

Zhang Maoyuan

Nanjing Science and Technology University

Abstract:

This paper aims to use the industry life cycle theory and the ARCH model to analyze and predict the change rate of the federal funds rate, and thus to judge the development stage and future trend of American capitalism. The paper first comprehensively analyzes the division, characteristics and relationship between the Federal Reserve's federal funds rate change cycle and economic recession phenomena of the life cycle stages of capitalism, and points out that American capitalism has entered the recession stage. Then, using the monthly return data of the federal funds rate from July 1, 1954 to November 2023, the ARCH(2) autoregressive conditional heteroscedasticity model is established to dynamically predict the change rate of the federal funds rate. It is found that the trend of the US interest rate hike will not continue to strengthen, but will gradually weaken, and may eventually enter the interest rate cut cycle, which is consistent with the historical cycle, and there are economic recession phenomena accompanying it. This result is consistent with the judgment of the life cycle theory. The significance of this paper lies in: applying the ARCH model to the analysis and prediction of the change rate of the federal funds rate, and comparing the development of capitalism to the industry life cycle, from two different perspectives, different dimensions of theoretical and empirical analysis, to carry out a more accurate analysis of the development of American capitalism, so as to better grasp the development law of capitalism.

Key Words:

ARCH model; Life cycle theory; Economic recession; Federal benchmark interest rate; Interest rate hike.

引言

美国作为资本主义的代表国家，其联邦基金利率的变化对全球经济和政治有着重要的影响，而联邦基金利率的变化又反映了美国资本主义的发展阶段和未来趋势。过去68年间每次美联储“加息-降息”的周期后，美国都出现了不同程度的经济衰退现象^[1]^。截至目前，美联储的加息趋势有所减缓，意味着很有可能当前美联储即将进入降息周期，美国经济是否会再次面临衰退的困境，是全世界学者关注的焦点。因此，分析预测联邦基金利率的变化率，可以帮助我们更好地理解和应对美国资本主义的衰退和崛起。如今，随着产业经济学和计量经济学发发展与普及，对行业的生命周期理论以及对时间序列数据波动率预测的相关理论已经发展得十分完善，基于对美联储联邦基金利率的分析，从而判断美国经济形势的走向方面也有较多应用，但普遍的问题是：对美国经济走势的分析角度局限于近现代几十年的范围，缺乏对事物的发展规律的总体分析与研究。

有鉴于此，本文有三个目的：一是借用行业的生命周期理论，综合分析资本主义的生命周期阶段的划分、特征等，并阐述美联储联邦基金利率变动周期与经济衰退现象的伴生性，结合实例指出美国当前已经处于衰退阶段；二是利用ARCH模型来分析预测联邦基金利率的变化率，从而判断美联储当前是否即将进入降息周期，未来是否可能再次发生经济衰退现象。

本文余下内容部分安排如下：第二部分利用文献综述阐述生命周期理论在资本主义的应用，对每个阶段进行时间的划分、特点的提炼、总结，在此基础上对经济衰退现象和美联储“加息-降息”周期伴生现象进行分析，向读者展示当前美联储持续加息的背景下，未来是否会进入降息周期的可能性需要基于对联邦基金利率波动情况的预测来展开。第三部分对联邦基金利率建立ARCH(2)条件异方差模型进行实证分析，基于历史数据对未来15个月的变动情况做出预测。第四部分基于前文的分析，最终得出结论。

文献综述

资本主义

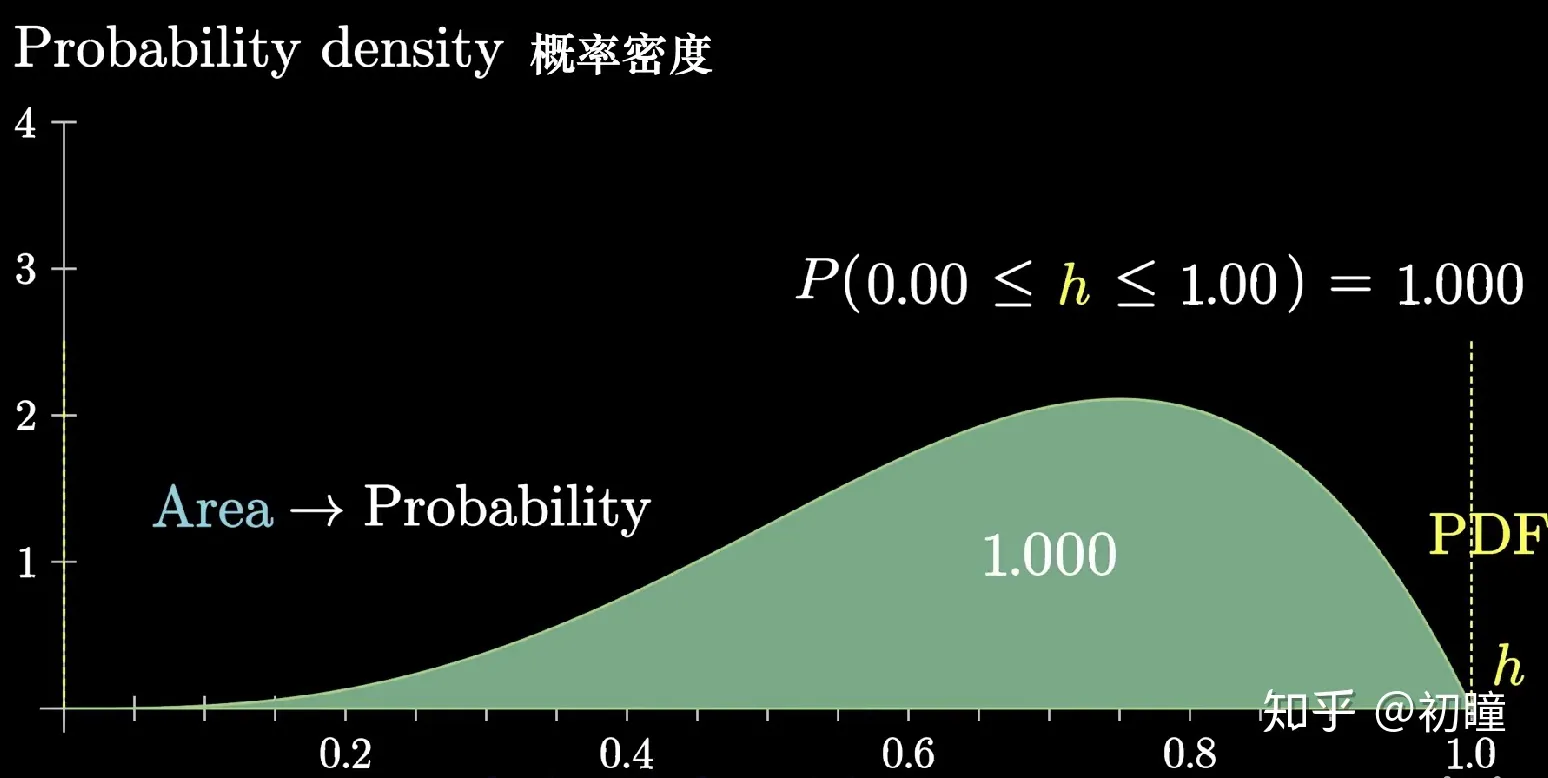
产业经济学的生命周期理论是一种分析行业发展变化的重要工具，它将一个行业从兴起到衰落分为四个阶段：幼稚期、成长期、成熟期和衰退期。这一理论不仅可以用于描述和预测单个行业的演进过程，也可以用于比较和解释不同行业之间的差异和联系。本文试图将产业经济学的生命周期理论应用于资本主义发展阶段的分析，探讨资本主义作为一种社会经济制度，是否也具有类似于行业的生命周期特征，以及这一理论对于理解和评价当代资本主义的现状和前景有何启示。

图 1 行业生命周期

资本主义是一种以私有制为基础，以市场为调节机制，以利润为动力的经济体制，它自从中世纪在欧洲城市萌芽以来，经历了几个不同的发展阶段，包括原始资本主义、工业资本主义、垄断资本主义、福利资本主义和数字资本主义3。这些阶段的划分，主要依据的是资本主义的生产方式、交易方式、竞争状况、技术水平、政治制度等方面的变化。从这个角度看，资本主义的发展历程，与产业经济学的生命周期理论有着相似之处，都是由创新、扩张、稳定和衰退等阶段组成的动态过程。因此，我们可以借用产业经济学的生命周期理论，来分析资本主义的发展规律和趋势。

首先，资本主义的幼稚期，相当于原始资本主义阶段，大约从14世纪到17世纪，这一阶段的主要特征是商品经济的出现和发展，商业资本的积累，海外殖民的扩张，以及资产阶级革命的爆发4。这一阶段的资本主义，还没有形成完整的生产方式和市场体系，而是在封建社会的基础上，逐渐孕育和成长的。在这一阶段，资本主义的创新主要表现在对封建制度的冲击和破坏，以及对新兴市场的开拓和探索。

其次，资本主义的成长期，相当于工业资本主义阶段，大约从18世纪到19世纪，这一阶段的主要特征是工业革命的发生和推进，工厂制的建立和普及，自由贸易的兴起和扩展，以及资本主义国家的竞争和争霸5。这一阶段的资本主义，已经确立了自己的生产方式和市场体系，而且在全球范围内迅速发展和传播。在这一阶段，资本主义的创新主要表现在对生产力的提升和改造，以及对世界市场的整合和控制。

再次，资本主义的成熟期，相当于垄断资本主义和福利资本主义阶段，大约从19世纪末到20世纪末，这一阶段的主要特征是金融资本的形成和集中，垄断组织的出现和壮大，国家干预的增加和深化，以及社会福利的提高和扩大6。这一阶段的资本主义，已经达到了自己的生产方式和市场体系的高度完善和发展，而且在全球范围内形成了相对稳定的格局和秩序。在这一阶段，资本主义的创新主要表现在对生产关系的调整和改良，以及对社会矛盾的缓解和化解。

最后，资本主义的衰退期，相当于数字资本主义阶段，大约从21世纪初至今，这一阶段的主要特征是信息技术的革命和普及，数字经济的崛起和扩张，全球化的危机和挑战，以及社会不平等的加剧和爆发7。这一阶段的资本主义，已经遇到了自己的生产方式和市场体系的重大变革和危机，而且在全球范围内面临着激烈的竞争和冲突。在这一阶段，资本主义的创新主要表现在对新兴技术的利用和掌握，以及对新型市场的开发和占领。

综上所述，我们可以看出，资本主义的发展历程，与产业经济学的生命周期理论有着相似之处，都是由创新、扩张、稳定和衰退等阶段组成的动态过程。这一理论对于理解和评价当代资本主义的现状和前景有一定的启示作用。例如，我们可以从中发现，资本主义的发展并非是一条单向的、无限的、永恒的曲线，而是一条波动的、有限的、有始有终的曲线。资本主义的发展，不仅受到内部的生产力和生产关系的制约，也受到外部的自然环境和社会环境的影响。资本主义的发展，不仅带来了经济的增长和社会的进步，也带来了危机的爆发和矛盾的激化。资本主义的发展，不仅需要不断的创新和变革，也需要合理的调节和平衡。因此，我们不能盲目地崇拜或否定资本主义，而应该客观地分析和评价资本主义，以及寻求超越资本主义的可能性和途径。

美国的高利贷帝国主义与资本主义的衰退

美国的高利贷帝国主义是指美国在21世纪初以来，利用其金融、军事、政治等优势，通过高利贷、制裁、战争等手段，对全球的发展中国家和弱小国家进行剥削和控制的一种新型的帝国主义。美国的高利贷帝国主义有以下的特征：

以金融资本为主导，以美元为武器，通过国际金融机构和金融市场，对全球的货币、债务、贸易、投资等进行操纵和干预，从而获取高额的利润和利息。
以军事力量为支撑，以反恐为借口，通过军事基地和军事同盟，对全球的战略要地和资源富集地进行威慑和干涉，从而维护其霸权地位和利益。
以政治影响为辅助，以民主为幌子，通过政治组织和政治运动，对全球的政治制度和政治秩序进行改造和破坏，从而扩大其话语权和势力范围。

美国的高利贷帝国主义与资本主义的衰退有着密切的关系，可以从以下的方面进行分析：

美国的高利贷帝国主义是资本主义的衰退的表现，因为它反映了美国的实体经济的萎缩和虚拟经济的膨胀，以及美国的生产力的下降和金融资本的过剩，导致美国不得不通过对外输出资本和危机，来解决其内部的矛盾和问题。
美国的高利贷帝国主义是资本主义的衰退的原因，因为它加剧了全球的经济不平衡和不稳定，以及全球的政治冲突和动荡，导致全球的经济增长和发展受到严重的阻碍和挑战，从而影响了资本主义的进一步发展和完善。
美国的高利贷帝国主义是资本主义的衰退的结果，因为它引发了全球的反帝反霸的斗争和反抗，以及全球的多极化和多元化的趋势和发展，导致美国的霸权地位和优势受到严重的削弱和挑战，从而威胁了资本主义的统治和生存。

美联储联邦基金利率与美国经济衰退的关系

美联储联邦基金利率是指美国银行之间借贷联邦基金（即美联储账户上的超额准备金）的无担保隔夜利率，它是美联储实施货币政策的主要工具，也是影响美国和全球金融市场的重要参考。美联储联邦基金利率的变化会影响美国的通胀、就业、经济增长等经济指标，从而影响美国的经济状况和衰退的可能性。

美联储联邦基金利率的历史变化可以分为以下几个阶段：

1954年至1979年：自由浮动期，美联储联邦基金利率随着市场供求的变化而波动，没有明确的目标和范围，反映了美国经济的高速增长和高通胀的特征。
1979年至1982年：货币目标期，美联储联邦基金利率以货币供应量为目标，通过调节货币供应量来控制利率，反映了美国经济的滞胀和危机的特征。
1982年至2008年：利率目标期，美联储联邦基金利率以利率为目标，通过调节利率来影响货币供应量，反映了美国经济的稳定增长和低通胀的特征。
2008年至2015年：零利率期，美联储联邦基金利率降至接近零的水平，通过量化宽松等非常规措施来刺激经济，反映了美国经济的衰退和危机的特征。
2015年至今：正常化期，美联储联邦基金利率逐步提高，通过缩减资产负债表等常规措施来收紧货币政策，反映了美国经济的复苏和增长的特征。

美联储联邦基金利率可以视为时间序列模型，利用其历史数据分析得出规律性。时间序列模型是一种用来描述和预测时间序列数据的统计模型，它可以分为趋势、季节、周期和随机四个成分。美联储联邦基金利率的时间序列模型可以用以下的公式表示：

$r_t = T_t + S_t + C_t + e_t$

其中， $r_t$ 是第 $t$ 期的美联储联邦基金利率， $T_t$ 是第 $t$ 期的趋势成分， $S_t$ 是第 $t$ 期的季节成分， $C_t$ 是第 $t$ 期的周期成分， $e_t$ 是第 $t$ 期的随机成分。

根据美联储联邦基金利率的历史数据，可以用以下的方法来估计和预测其时间序列模型的各个成分：

趋势成分：可以用移动平均法或指数平滑法来估计和预测美联储联邦基金利率的长期趋势，反映了美联储的货币政策取向和目标。
季节成分：可以用季节差分法或季节指数法来估计和预测美联储联邦基金利率的季节波动，反映了美国经济的季节性变化和需求。
周期成分：可以用谱分析法或自回归移动平均法来估计和预测美联储联邦基金利率的周期波动，反映了美国经济的周期性变化和危机。
随机成分：可以用白噪声检验法或残差分析法来估计和预测美联储联邦基金利率的随机波动，反映了美国经济的不确定性和风险。

根据美联储联邦基金利率的加息-减息周期性变动与美国经济衰退伴随出现的现象，可以对未来联邦基金利率进行分析预测，从而判断经济衰退在近期发生的概率。一般来说，美联储联邦基金利率的加息-减息周期可以分为以下几个阶段：

加息阶段：美联储联邦基金利率逐步提高，反映了美国经济的增长和通胀的压力，以及美联储的收紧货币政策的意图。这一阶段通常持续较长时间，对经济的影响是滞后的，可能导致经济的过热和泡沫的形成。
顶点阶段：美联储联邦基金利率达到最高点，反映了美国经济的高峰和通胀的峰值，以及美联储的观望货币政策的态度。这一阶段通常持续较短时间，对经济的影响是同步的，可能导致经济的转折和危机的爆发。
减息阶段：美联储联邦基金利率逐步降低，反映了美国经济的衰退和通胀的下降，以及美联储的宽松货币政策的意图。这一阶段通常持续较长时间，对经济的影响是滞后的，可能导致经济的复苏和增长的恢复。
谷底阶段：美联储联邦基金利率达到最低点，反映了美国经济的低谷和通胀的谷底，以及美联储的观望货币政策的态度。这一阶段通常持续较短时间，对经济的影响是同步的，可能导致经济的转折和增长的开始。

根据美联储的最新公告，美联储联邦基金利率目前的水平和未来走势如下：

水平：根据美联储的最新公告，美联储联邦基金利率目前的目标区间为5.25%至5.50%，较上次会议上调了50个基点。这是美联储今年以来连续第八次加息，累计加息475个基点。
走势：根据美联储的最新经济前景预期，美联储联邦公开市场委员会多数成员认为，今年联邦基金利率目标区间或升到5.5%至5.75%之间。这意味着，在今年剩下的两次货币政策会议上，美联储可能最多再加息一次。此外，多数成员预计美联储将在2024年降息。

根据历史数据，可以发现美联储联邦基金利率的加息-减息周期与美国经济衰退的发生有着密切的关系，美联储联邦基金利率通常在加息-降息的周期性变动后，美国经济衰退的概率会大幅增加，而在美联储联邦基金利率平稳变动情况下，美国经济衰退的概率会大幅降低。因此，可以根据美联储联邦基金利率的当前水平和未来走势，来预测美国经济衰退在近期发生的概率。

实证分析

数据来源以及描述性统计

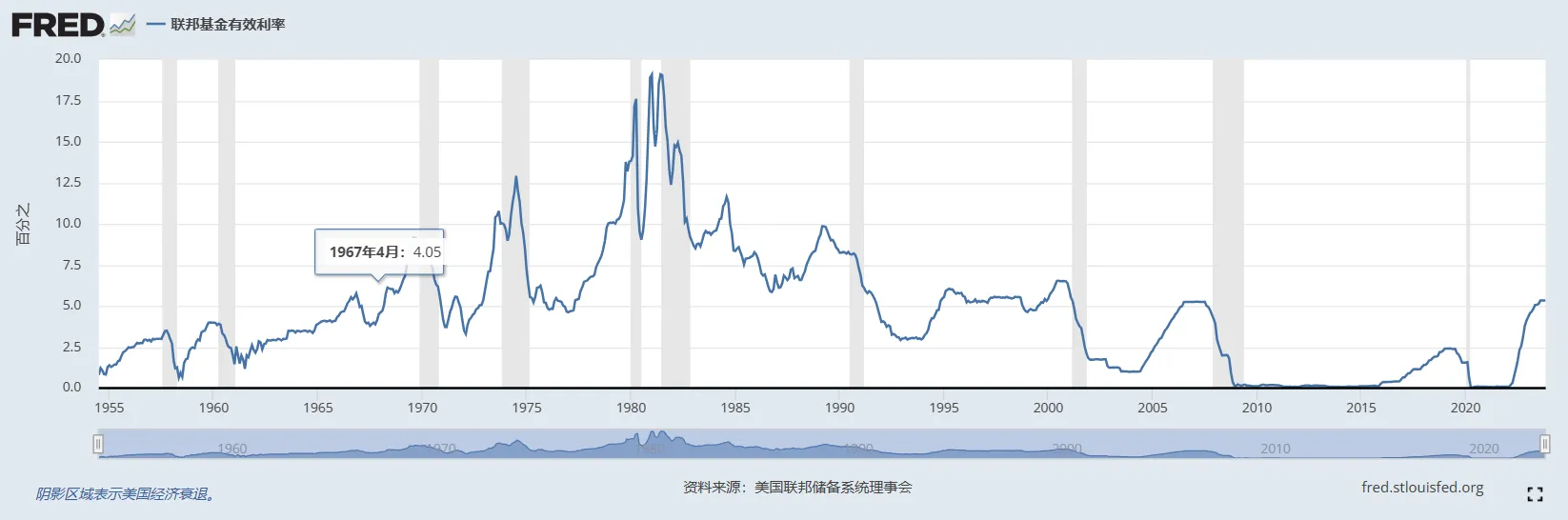
本文使用的数据是美联储经济在线数据数据库（FRED）提供的1954年7月1日至2023年11月的联邦基金利率月度收益率的数据，共计833个观察值。联邦基金利率是美国银行间短期拆借市场上的利率，是美联储实施货币政策的主要工具，也是全球金融市场的重要参考利率。联邦基金利率的变化率可以反映美国货币政策的调整方向和力度，以及美国经济的状况和预期。本文选择这个时间段的数据，是因为它涵盖了现代美国资本主义的主要发展阶段，体现了美联储的不同货币政策周期，可以更好地反映联邦基金利率的变化规律和特征。本文使用的数据来源于美联储官方的数据库，具有较高的可信度和准确性。本文使用的联邦基金利率的变化率是指联邦基金利率的收益率，即：

$r_t=\frac{F_t-F_{t-1}}{F_{t-1}}$

其中， $r_t$ 表示第 $t$ 期的联邦基金利率的变化率， $F_t$ 表示第 $t$ 期的联邦基金利率。

表 1 展示了联邦基金利率的变化率的描述性统计结果，可以看出，联邦基金利率的最小值为 0.0500，最大值为 19.10，平均值为 4.601，标准差为 3.595。它的下四分位数为 1.800，中位数为 4.160，上四分位数为 6.240。进行一阶差分并求出变化率后，方差得到了有效降低。表明联邦基金利率的变化不服从正态分布，存在较大的波动和异常值。这些统计特征说明联邦基金利率受到了美国经济和政治的多重影响，具有较高的不确定性和不稳定性，同时也反映了美国资本主义的发展阶段的变化和特征，如在衰退期，联邦基金利率的变化率会出现较大的负值，而在复苏期，联邦基金利率的变化率会出现较大的正值，等等。

VARIABLES	N	min	p25	p50	mean	p75	max	sd
$F_t$	833	0.0500	1.800	4.160	4.601	6.240	19.10	3.595
$r_t$	832	-0.923	-0.0248	0.00225	0.0132	0.0403	1.500	0.149

表 1 联邦基金利率原数据及变化率的描述性统计

图 2 展示了联邦基金利率变动与美国经济衰退现象在时间上的分布特点，描述了美国经济衰退现象（阴影区域）与联邦基准利率变动（美联储“加息-降息”周期）伴随出现的现象，美国在过去68年间的九次经济衰退都是随着“加息-降息”式的联邦基准利率调整周期出现的。

图 2 联邦基金利率与经济衰退的时序图

基于联邦基金利率计算出其波动率，图 3 展示了联邦基金利率的变化率的时序图，可以看出，联邦基金利率的变化率存在明显的波动集群现象，即高波动期和低波动期交替出现，这表明联邦基金利率的变化率存在条件异方差的特征，直接使用OLS普通最小二乘估计会产生较大误差。因此，可以使用ARCH模型来进行分析和预测。

图 3 联邦基金利率的变化率的时序图

ARCH模型的建立

ARCH模型简介

目前，预测类似关于变动率时间序列的预测方法很多，比较经典的有灰色理论、趋势预测、时间序列的分解、指数平滑法等，这些方法对于经济形势的长期预测比较准确，而对短期趋势的把握度不高。

与这些方法相比，Robert Fry Engle III在1982年的《Econometrica》上提出的ARCH模型能解决时间序列的波动性问题，更适合用于美联储联邦利率的发展趋势分析预测。ARCH模型是一种用来描述时间序列方差变化的模型。ARCH模型的基本思想是，某个时点的方差不仅取决于该时点的误差平方，还取决于过去的方差。ARCH模型即为条件异方差自回归模型，核心思想是通过分析时间序列数据的历史误差平方项与序列值之间的相关性，来解释序列条件异方差这种波动率不为常数的状况，准确地模拟时间序列变量的波动性的变化，从而更准确地把握分析对象的风险情况。

古典假定中随机扰动项 $\varepsilon_t$ 是同方差的，所以残差作为随机扰动项的估计，应该是同方差的，不应该有条件异方差性，残差的波动率 $\sigma_t^2$ 应该是一个常数，而不应该是一个关于 $t$ 的变量。

而在ARCH模型中，残差 $u_t$ 存在波动集群的性质表示为：残差 $u_i$ 在 $t$ 时刻的方差 $\sigma^2_t$ 和历史q期的残差平方 $u_{t-i}^2$ 存在序列相关性（并且是同向的），并且 $u_i^2$ 自身是服从AR(q)自回归自相关的，就可以用历史q个时刻上的残差平方 $u_{t-i}^2$ 存在作为解释变量去回归方差 $\sigma^2_t$ 。此时作为解释变量的历史残差平方项 $u_{t-i}^2$ 就不能是白噪声，否则就会因为具有随机性，无法预测被解释变量波动率 $\sigma^2_t$ ，没有预测意义。据此，有ARCH效应的模型在数学上定义为：

残差自身 $u_i$ 存在条件异方差性，不是白噪声，存在关系 $u_i=\sigma_tv_t$ ， $v_t$ 是一个白噪声；
残差的方差 $\sigma_t^2$ 和残差滞后项的平方 $u_{t-i}^2$ 存在q阶序列相关，因此方差不是恒定的常数，不是白噪声；
残差的平方 $u_{t-i}^2$ 存在q阶自相关，不是白噪声。实质上是 $u_t^2$ 服从 AR(q)， $u_t^2$ 不是整个序列上都没有自相关（有q期自相关）。

$\varepsilon_t=\mu v_t \\ \sigma_t^2=a_0+a_1\varepsilon_{t-1}^2+\cdots+a_q\varepsilon_{t-q}^2 \\ u_t^2=\alpha_0+\alpha_1 u_{t-1}^2+ \cdots + \alpha_0 u_{t-q}^2 + v_t$

其中 $v_t$ 是 $u_t^2$ 的独立同分布的随机误差项，是白噪声。同时，为了保证 $u_t^2$ 是非负数， $a_0\ge0$ ， $\sum_{i=1}^q a_i<1$ ， $a_i>0(i=1, 2, 3\cdots , q)$

上式表明，如果一个序列的残差历史值的平方存在自回归自相关效应，那么序列残差的方差和残差历史值平方项就存在序列相关性，因此可以对方差做出预测。

平稳性检验

此前的图2和图3显示了联邦基金利率的原序列的和一阶差分序列的变化趋势。从图中可以看出，原序列呈现出明显的上升和下降的波动，而一阶差分序列则相对稳定，围绕零线波动。接下来，利用联邦基金利率的月度数据，对其进行平稳性检验。首先，对原序列和一阶差分序列分别进行自相关系数分析和偏自相关系数分析，发现原序列的自相关系数和偏自相关系数均呈现出缓慢衰减的趋势，而一阶差分序列的自相关系数和偏自相关系数则在滞后阶数较小的范围内显著，且在滞后阶数较大时接近于零。这表明原序列可能存在单位根，而一阶差分序列则是平稳的。

	检验统计量	1%	5%	10%
$Z(t_F)$	-2.097	-3.430	-2.860	-2.570
$Z(t_r)$	-21.798	-3.430	-2.860	-2.570

表 2 原序列和一阶差分序列的ADF单位根检验结果

为了进一步验证这一推断，本文对原序列和一阶差分序列进行了ADF单位根检验，检验结果如表 2 所示。从表 2 中可以看出，原序列的ADF检验统计量为-2.097，大于1%、5%和10%的临界值，因此不能拒绝原序列存在单位根的原假设，即原序列是非平稳的；一阶差分序列的ADF检验统计量为-21.798，小于1%、5%和10%的临界值，因此可以拒绝一阶差分序列存在单位根的原假设，即一阶差分序列是平稳的。这一结果与自相关系数分析和偏自相关系数分析的结果一致。

ARCH效应检验

本文以ARCH(2)模型预测了残差，并计算其平方项序列。分析残差以及残差平方各自的自相关性、偏自相关性，发现残差平方偏自相关系数二阶截尾，自相关系数三阶拖尾，有很显著的自回归自相关性。因此，可以考虑建立ARCH(2)或ARCH(3)模型。进一步分析，原序列不平稳，因此使用ARCH-LM法检验一阶差分序列的ARCH(q)效应，结果显示在之后10阶范围内均存在ARCH效应，说明联邦基金利率变化率存在条件异方差效应，可以建立相应模型进行分析、预测。ARCH-LM法是一种基于残差平方的LM检验，它可以检验时间序列是否存在ARCH效应，即残差的方差是否依赖于其历史值。ARCH-LM法的原假设是不存在ARCH效应，即残差平方的自回归系数为零，如果检验统计量大于临界值，或者p值小于显著性水平，就拒绝原假设，认为存在ARCH效应。本文选择10阶范围内，是因为一般认为10阶以内的滞后项对方差的影响较为显著，而超过10阶的滞后项对方差的影响较为微弱。检验结果符合本文的预期，因为从图 3 中也可以看出联邦基金利率的变化率存在明显的波动集群现象，即条件异方差的特征。

lags§	chi2	df
1	40.763	1
2	128.173	2
3	128.228	3
4	140.023	4
5	141.050	5
6	145.560	6
7	146.550	7
8	147.137	8
9	147.113	9
10	147.067	10

表 3 变化率序列ARCH-LM检验结果

ARCH模型定阶

从模型设定上看，ARCH模型的定阶取决于残差历史平方项自回归自相关的滞后范围。如果残差的平方存在自回归自相关，那么残差的方差就必定不是常数，也就是存在条件异方差的现象。本文在实际应用过程中，首先利用VAR§模型来检验时间序列的自回归性，表 2 的结果表明，大部分标准下均选择滞后2阶。

lags	LL	LR	df	p	FPE	AIC	HQIC	SBIC
0	411.802			.021602	-.997093	-.994899	-.991372
1	447.865	72.126	1	0.000	.01984	-1.0822	-1.07781	-1.07076
2	457.201	18.672*	1	0.000	.019442	-1.10243	-1.09585*	-1.08527*
3	458.244	2.0858	1	0.149	.01944*	-1.10253*	-1.09376	-1.07965
4	458.622	.75576	1	0.385	.01947	-1.10102	-1.09005	-1.07242
5	458.743	.24244	1	0.622	.019511	-1.09889	-1.08572	-1.06457
6	460.015	2.5437	1	0.111	.019498	-1.09955	-1.08419	-1.0595
7	460.07	.11041	1	0.740	.019543	-1.09726	-1.0797	-1.05149
8	460.444	.74787	1	0.387	.019573	-1.09574	-1.07599	-1.04425

表 4 VAR(8)模型分析

另一方面，对AR(6)模型进行回归分析，结果如表 5 ，也能发现自回归在二阶后不显著。因此自回归模型选择AR(2)模型。

变量	Coefficient	Std. err.	t	P>\|t\|	[95% conf. interval]
L1.	0.2401785	0.0348994	6.88	0.000	0.1716758, 0.3086812
L2.	0.1343625	0.0355224	3.78	0.000	0.064637, 0.2040881
L3.	0.0544009	0.03581	1.52	0.129	-0.0158892, 0.124691
L4.	-0.0369586	0.0357131	-1.03	0.301	-0.1070586, 0.0331413
L5.	0.0065668	0.0354361	0.19	0.853	-0.062989, 0.076123
L6.	0.0473288	0.0341384	1.39	0.166	-0.0196803, 0.1143379

表 5 AR(6)模型分析

确定序列值有AR(2)二阶自回归自相关，在此基础上分别计算1阶、2阶、3阶、4阶的ARCH模型的BIC、AIC值。BIC和AIC是两种常用的信息准则，它们可以用来比较不同模型的拟合优度，一般来说，BIC和AIC值越小，说明模型越优。综合判断信息准则，选择建立ARCH(2)模型。

Variable	model1	model2	model3	model4
g1
L1.	0.30628305	0.31645871	0.32809236	0.31815545
L2.	0.12988576	0.10266357	0.10669246	0.08474826
_cons	0.00120953	0.01020873	0.01000047	0.01089089
ARCH
L1.	0.8585313	0.28364785	0.27994483	0.27026857
L2.		0.45064878	0.43525708	0.45615508
L3.			0.01475149	0.01740073
L4.				-0.01819091
_cons		0.00795035	0.00788607	0.00799376
Statistics
aic		-1285.3931	-1284.8226	-1287.8041
bic		-1257.0645	-1251.7726	-1250.0327

表 6 不同阶数ARCH模型BIC、AIC对比

根据表 6 的不同阶数的ARCH模型的信息准则进行分析，本文选择ARCH(2)模型，是因为它在BIC和AIC值上都优于其他阶数的模型，而且也符合经济学的常识，即联邦基金利率的变化率的方差受到其近两期的历史值的影响，而更远期的历史值的影响可以忽略。综上所述本文建立的ARCH(2)模型的具体形式为：

$r_t = \mu+ \beta_1r_{t-1}+\beta_{t-2}r_{t-2}+\varepsilon_t \\ \varepsilon_t=\sigma_t v_t \\ \sigma^2_t=a_0+a_1\varepsilon_{t-1}^2+a_2\varepsilon_{t-2}^2$

其中， $\beta_i$ 是 $r_t$ 滞后项的系数， $a_i$ 是 $\varepsilon_t$ 滞后项的系数， $v_t$ 是独立同分布的白噪声序列。

ARCH模型的显著性

基于建立的ARCH(2)模型，本文使用折线图来展示预测值和真实值的对比，是为了直观地显示模型的预测能力和精度。从图 6 、图 5 、图 6 都可以看出，变化率的预测值和真实值的走势基本一致，且预测误差较小，说明模型能够较好地捕捉联邦基金利率的变化率的波动特征。

最近的加息周期是从2020疫情爆发后开始的，因此图 4 展示了2020年1月至2023年11月的预测值及95%的置信区间与真实值的折线图对比情况，可以看出，变化率的预测值在2022年5月的峰顶后，呈现出逐渐下降的趋势，且置信区间较为收敛，表明预测结果较为稳定和可靠，同时图 4 置信区间范围在波动剧烈时明显更宽，说明本文建立的条件异方差模型能有效描述波动集群的特征。图 5 显示了长期的变化率折线图，同样明显的表现了波动集群的特征。图 6 利用预测的联邦基金利率变化率计算出联邦基金利率的预测值，也能直观显示模型有较强的预测能力和精度。


图 4 短期内带有置信区间的变化率预测值与真实值的对比折线图	图 5 长期变化率预测值与真实值的对比折线图	图 6 长期联邦基金利率的预测值与真实值的对比折线图

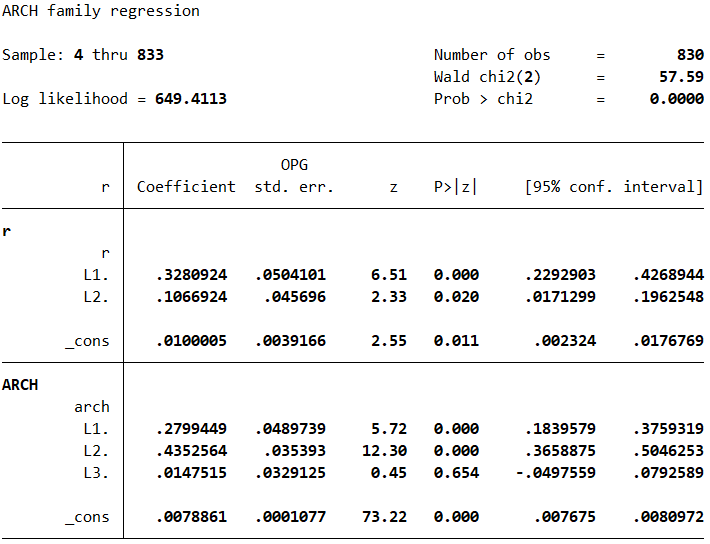
对ARCH模型进行回归分析，ARCH滞后一阶项和二阶项系数显著不为零，滞后三阶项不显著，同时ARCH(2)模型Wald系数远大于临界值，概率远小于显著性水平，拒绝模型系数为零的原假设。另外，ARCH(2)似然函数值为648.6966大于ARCH(3)似然函数值647.5277，综合分析本文建立的ARCH(2)模型是显著的。


图 4 短期内带有置信区间的变化率预测值与真实值的对比折线图	图 5 长期变化率预测值与真实值的对比折线图

同时，根据上文中表 6 不同阶数ARCH模型BIC、AIC对比对各阶数下信息准则的计算，也都能看出ARCH模型的显著性很强，对于联邦基金利率的预测有明显的应用意义。

综上所述，这些结果都表明：模型的契合度非常高，预测结果有实际意义，因为它可以帮助我们判断美国货币政策的调整方向和力度，以及美国经济的状况和预期，从而为我们分析美国资本主义的发展阶段和未来趋势提供依据。

ARCH模型的预测

从生命周期理论的角度，美国资本主义已经进入了衰退期，经济增长放缓，通货膨胀加剧，债务危机加深，社会矛盾激化，因此，美联储不得不采取宽松的货币政策，降低联邦基金利率，以刺激经济活动，缓解金融压力，维持社会稳定。从现实情况的角度，美国受到了新冠疫情的严重冲击，经济陷入了深度衰退，失业率飙升，贫富差距扩大，政治分裂加剧，因此，美联储不得不采取前所未有的量化宽松措施，将联邦基金利率降至接近零的水平，以应对经济危机，支持市场信心，抵御外部冲突。基于建立的 ARCH(2) 模型，本文对联邦基金利率的变化率进行了动态预测，向未来扩展了 15 期，即从 2023 年 12 月开始预测至 2025 年 2 月结束，结果如图 7 。

图 7 联邦基金利率的变化率的预测值和置信区间

预测结果的含义和逻辑是：美国加息的趋势不会继续加强，而是会呈现逐渐减弱的趋势，最终可能会进入降息周期。这一现象符合我们此前利用生命周期理论对美国资本主义的发展阶段和未来趋势的判断，也与现实情况发展一致。

结论

本文利用行业的生命周期理论和 ARCH 模型来分析预测联邦基金利率的变化率，从而判断美国资本主义的发展阶段和未来趋势。本文的主要结论和贡献如下：

本文将资本主义的发展类比为行业的生命周期，从两个不同的角度来对美国资本主义的发展展开分析。一方面，从宏观的历史视角，综合分析了资本主义的生命周期阶段的划分、特征和美联储联邦基金利率变动周期与经济衰退现象的关系，指出美国资本主义已经进入了衰退期，未来可能会再次陷入经济危机。另一方面，从微观的数据视角，本文利用 ARCH 模型来分析预测联邦基金利率的变化率，发现美国加息的趋势不会继续加强，而是会逐渐减弱，最终可能会进入降息周期，这一结果与生命周期理论的判断相一致。
本文将 ARCH 模型应用于联邦基金利率的变化率的分析预测，以及将资本主义的发展类比为行业的生命周期，从两个不同的角度、不同维度的理论、实证分析的结合，来对美国资本主义的发展展开更加准确的分析，从而更好地把握资本主义的发展规律。本文的研究方法和结果不仅对理解美国资本主义的历史和现状有重要的理论意义，也对预测美国资本主义的未来和应对其影响有重要的实践价值。

本文的研究也存在一些局限和不足，如：ARCH 模型的假设和参数的选择可能存在一定的主观性和不确定性，联邦基金利率的变化率可能受到其他的因素和影响的干扰，美国资本主义的衰退可能有其他的判断和衡量的标准和方法，等等。本文的研究可以在未来进行一些扩展和深化，如使用其他的模型和方法来分析预测联邦基金利率的变化率，考虑其他的变量和因素对联邦基金利率的变化率的影响，对美国资本主义的衰退进行更多的实证分析和证据支持，以及对中国的社会主义经济发展提出更具体和可行的政策建议，等等。

参考文献

［1］高志刚. 《产业经济学（第二版）》 [M]. 北京: 中国人民大学出版社, 2020: 101-104.
［2］芮明杰. 《产业经济学（第二版）》 [M]. 上海: 上海财经大学出版社, 2012: 47.
［3］ Kondratieff N. Die Langen Wellen der Konjunktur [J]. Archiv fur Sozialwissenschaft und Sozialpolitik, 1926, 56: 573-609.
［4］ AKerman J, Sprigge E, Napier C. Economic Progress and Economic Crises [J]. Society of Plastics Engineers, 1932, 63: 121-142.
［5］ Biernacki R. The Origin of Capitalism [M]. New York: Monthly Review Press, 1999: 638-639.
［6］ Wood E M. The Origin of Capitalism: A Longer View [M]. London: Verso, 2002.
［7］张思奇, 马刚, 冉华. 股票市场风险、收益与市场效率: ——ARMA-ARCH-M 模型 [J]. 世界经济, 2000, (05): 19-28.
［8］董银霞. 上证综指基于 ARCH 模型的 VaR 风险价值测度分析 [J]. 会计之友, 2014, (11): 70-75.
［9］郑丽雅, 易宪容. 美联储货币政策重大转向及对金融市场的巨大影响 [J]. 学术界, 2022, (06): 113-128.
［10］马涛. 高通胀下的美国经济面临衰退风险 [J]. 人民论坛, 2023, (02): 92-95.
［11］陈莉. 二维 Copula 模型与 Bayes 估计法下美联储加息联动效应测度 [J]. 统计与决策, 2020, 36(03): 125-130.
［12］曹永福, 匡可可. 美联储加息与新兴市场资本流动: 历史经验分析 [J]. 北京工商大学学报(社会科学版), 2016, 31(01): 23-30.
［13］杨玉林. 金融危机前后的美联储货币政策调控方式演变 [J]. 金融发展研究, 2021, (09): 56-64.
［14］宋博, 陈万义. 基于 HP 滤波和 ARMA-GARCH 模型的人民币汇率趋势预测 [J]. 数学的实践与认识, 2017, 47(01): 70-78.
［15］张瑜. 美联储降息的可能性条件 [J]. 中国金融, 2023, (14): 87-88.

附录

核心期刊截图

第一篇

第二篇

第三篇

第四篇

第五篇

第六篇

使用代码

//-----------------------------------------------------
//数据处理
//设置时间序列数据索引
tsset date
//日期数据格式转换，我这里图方便本来就把日期序列写成整数序列
destring date, replace
//对原数据绘图
graph twoway line f date, ytitle("原数据") xtitle("时间")
//生成变化率序列，不用对数差分，因为对数差分结果很奇怪...
gen r = (f - l.f) / l.f

//描述性统计
summarize f, detail
outreg2 using f_stats.doc, replace sum(detail) keep(f) eqkeep(N min p25 p50 mean p75 max sd) title(FED_R Descriptive Statistics)
//对变化率绘图
graph twoway line r date, ytitle("变化率") xtitle("时间")

//-------------------------------------------------------
//平稳性检验
//分析自相关性、偏自相关性
ac f
ac r
pac f
pac r
//对变化率做adf单位根检验
dfuller r

//--------------------------------------------------------
//ARCH效应检验及定阶
//序列自回归性检验
varsoc r,maxlag(8)
//AR(6)回归
reg rise l(1/6).rise
//ARCH-LM检验
estat archlm,lags(1/6)
//比较不同阶数ARCH模型效果
arch r L(1/2).r, arch(1/1)
estimates store model1
arch r L(1/2).r, arch(1/2)
estimates store model2
arch r L(1/2).r, arch(1/3)
estimates store model3
arch r L(1/2).r, arch(1/4)
estimates store model4

estimates table model1 model2 model3 model4, stats(aic bic)
//预测残差
arch r L(1/2).r, arch(1/2)
predict et, residual
//分析残差的自相关
ac et

//--------------------------------------------------------
//模型预测，对比预测值与真实值
//利用ARCH(2)预测r及其标准差
arch r L(1/2).r, arch(1/2)
predict rhat, y
predict se, stdp
//计算置信区间
gen ciu = rhat + 1.96*se
gen cil = rhat - 1.96*se
//对比短期真实值和预测值，从816期即2022年5月开始,绘制有置信区间的真实值与拟合值对比折线图
twoway (rarea cil ciu date if date>=810 & date<=835, lcolor(pink) fcolor(gs12) lpattern(dash)) ///
       (line r date if date>=810 & date<=835, lcolor(blue) lpattern(solid)) ///
       (line rhat date if date>=810 & date<=835, lcolor(red) lpattern(solid)), ///
       legend(label(1 "95% 置信度") label(2 "真实值") label(3 "预测值")) ///
       ytitle("变化率") xtitle("时间") title("带有置信区间的真实值与拟合值对比折线图") 
//对比长期变化率预测值和真实值
line r rhat date, legend(label(1 "真实值") label(2 "预测值")) title("联邦基金利率的变化率的真实值和预测值的长期折线图对比")
//根据变化率计算出原序列预测值
generate fhat = L.f * (1 + rhat)
//对比长期原序列预测值和真实值
line f fhat date, legend(label(1 "真实值") label(2 "预测值")) title("联邦基金利率的真实值和预测值的长期折线图对比")

//--------------------------------------------------------
//动态预测（样本外）
tsappend, add(15)
arch r L(1/2).r, arch(1/2)
predict drhat, dynamic(825) y

//计算置信区间
gen dciu = drhat + 1.96*se
gen dcil = drhat - 1.96*se

//从2020年1月疫情爆发前一个月开始，对比真实值和预测值，以及动态预测走向,绘制有置信区间的真实值与拟合值对比折线图
twoway (rarea dcil dciu date if date>=816 & date<=843, lcolor(pink) fcolor(gs12) lpattern(dash)) ///
       (line r date if date>=816 & date<=843, lcolor(blue) lpattern(solid)) ///
       (line drhat date if date>=816 & date<=843, lcolor(red) lpattern(solid)), ///
       legend(label(1 "95% 置信度") label(2 "真实值") label(3 "预测值")) ///
       ytitle("变化率") xtitle("时间") title("带有置信区间的真实值与拟合值对比折线图")