引言
在前几章的内容中提出符合古典假设的线性回归模型,所谓古典假设是指:
简单线性回归基本假定
- 假定一
零均值假定,即随机扰动项的条件期望等于0
- 假定二
同方差假定,即对于每一个给定的 Xi,随机扰动项的条件方差都等于 σ2
Var(ui∣Xi)=E[ui−E(ui∣Xi)]2=E(ui2)=σ2
- 假定三
无自相关假定,即各个扰动项的逐次值互不相关,也可以说他们的协方差等于零
Cov(ui,uk)=E[ui−E(ui)]E[uk−E(uk)]={σ2,0,i=ki=k(i,k=1,2,3,⋯n)
也就是说,
Var(U)=σ20⋮00σ2⋮0⋯⋯⋱⋯00⋮σ2=σ2In
Cov(ui,Xi)=E[ui−E(ui)]E[Xi−E(Xi)]=0
这一假定说明解释变量和扰动项是各自独立影响被解释变量的,从而得以分清各自的影响多少
- 假定五
正态性假定,即随机扰动项ui∼N(0,σ2)
- 假定六
无多重共线性。假设各解释变量的观测值线性无关,此时矩阵X满秩,也就是Rank(X)=k,方阵XTX满秩,从而方阵XTX可逆
在这一部分,我们会研究放宽古典假设(多重共线性、异方差、自相关)的模型,了解它们的含义,学会对它们进行判断,并给出补救的办法。
多重共线性
类似于线性代数中不满秩或叫线性相关的概念,如果一列X上的Y被其余某列X上的Y表示,会导致估计不准确,方差无限大。
判断方法:
- 经验
- 轻微改变变量或观测值,β反应大
- 重要解释变量不显著
- 正负号和预期相反
- r2、F高,但 t 统计量不显著
- r2(相关系数)>0.8
- VIF(方差扩大因子)≥10,
VIF反应方差扩大的速度,VIF=1−r21
- 逐步回归,逐个放入变量,看是否对r2,F有改进同时t显著

补救方法:
- 剔除变量
- 增大样本容量
- 对数变换
- 截面数据和时序数据并用
- 逐步回归
- 观察
AIC赤池信息准则 SIC施瓦茨信息准则,变小说明改善了,反之亦然
异方差
类型:
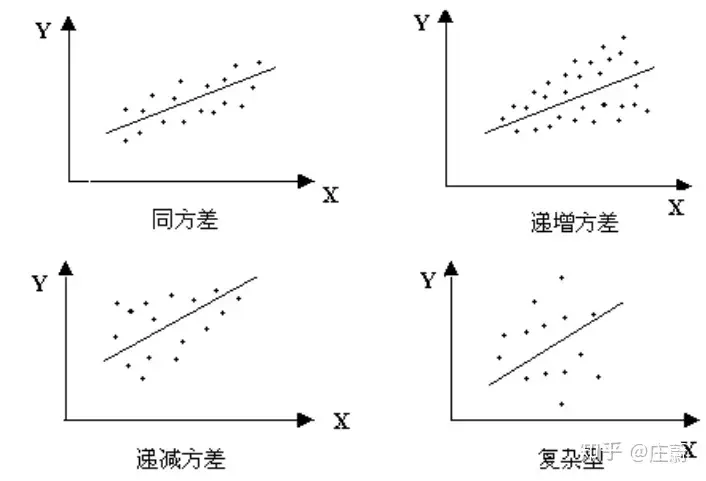
- 单调递增型:σi2 随X的增大而增大
- 单调递减型:σi2 随X的增大而减小
- 复杂型:σi2 与X的变化呈复杂形式

判断方法:
- 图示法
- X-Y 散点图,XY离散程度时大时小
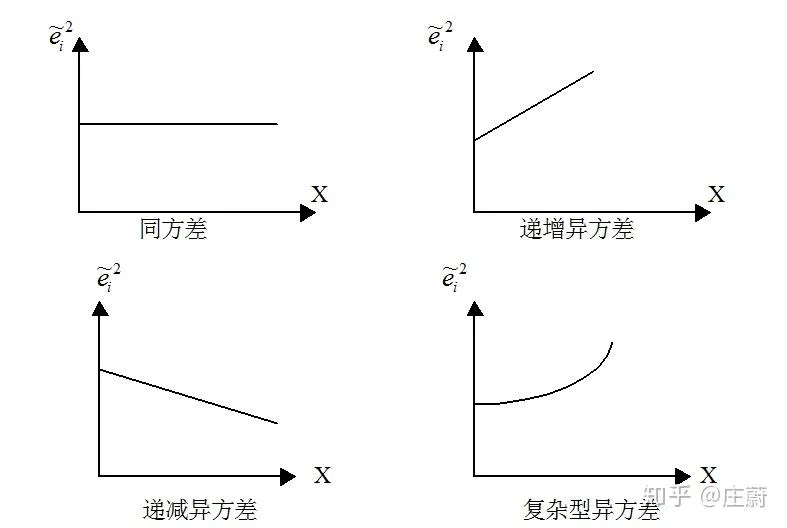
- X-e2 残差图,躺平的就是同方差,向上向下或者弯着走都是异方差

GQ检验 ,在大样本状态下如果满足除了同方差假设之外的其他假设,能看出是否有异方差
- 第一步,删掉 51 ~ 41 的数据,剩下数据对半分做回归
- 第二步,原假设前后两部分同方差
- 第三步,求两部分残差平方和,用 前∑ei2后∑ei2=样本F值
- 第四步,查自由度为 (2n−c−k) ,显著程度为 α 的边界F值
- 第五步,如果样本F值大于边界F值,拒绝原假设,存在异方差
White检验 针对时间序列数据,在大样本状态下如果满足除了同方差假设之外的其他假设,能看出是否有异方差,是由哪个变量引起
- 利用OLS求出残差平方 ei= ,利用各解释变量、变量平方、交叉乘积构造新变量,并且加上截距项 α ,干扰项 ,以及系数 βi ,做辅助回归
- 利用辅助回归的可决系数 r2 和样本容量 n 的乘积 nR2 ,推导出 [nR2∼χ2(新构造的解释变量个数)]
- 原假设:辅助回归各变量系数均为0
- 查自由度为p,显著水平为 α 的 χ2 边界值
- 如果 nR2>边界值,拒绝原假设,系数非0的变量引发异方差性
Glejser检验 在大样本状态下如果满足除了同方差假设之外的其他假设,能看出是否有异方差,是由哪个变量引起,以什么形式引起
- OLS求出 ei2,和某个可能引起异方差的变量 xi 自选一个模型(可以取 xi1 、 xi 、 xi1)做辅助回归,如果 β=0 ,且通过显著性检验,这个选择的变量确实以我们选择的模型形式引起异方差
ARCH检验 针对时间序列数据,在大样本状态下如果满足除了同方差假设之外的其他假设,能看出以p为滞后阶数的时间序列数据的异方差
- 利用OLS求出残差平方 ei2 ,计算其滞后序列 et2, et−12, ⋯, et−p2
- 做 e^t2=α0^+α1^et−12+α2^et−22⋯+αp^et−p2 的辅助回归
- 算 (n−p)R2,[(n−p)R2∼χ2(解释变量个数)],查自由度为p,显著性水平为 α 的 χ2 边界值
- 原假设:个解释变量系数 αi 都等于0
- $(n-p)R^2 > 边界值 $ ,拒绝原假设,存在异方差性
补救方法:
-
加权最小二乘法WLS

-
模型变换
- 在
WLS中设置了权数 wi=σ21,其实也可以设成其他东西,例如换成Xi 、Xi2、 (a0+a1Xi)2
-
对数变换
- 可以削弱异方差,但回归后的lnX和lnY是线性相关,X和Y就不是了
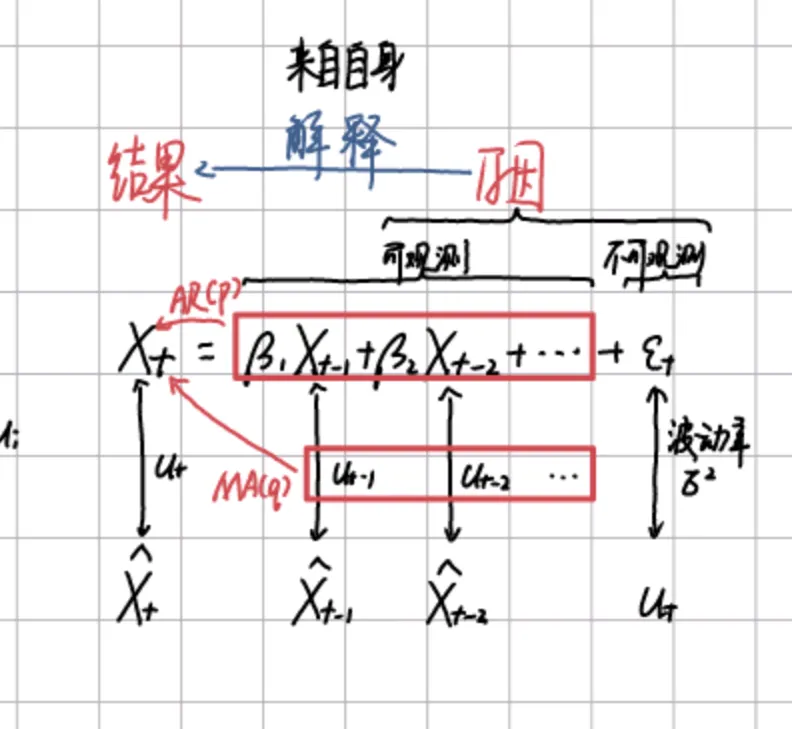
自相关性(序列相关,针对随机误差项 μ)
只看两期,看当期和滞后期之间的相关程度,

判断:
-
图示法

-
DW法
- n>15
- 解释变量非随机
- 随机误差项一阶自回归
- 模型右边没有Yt−1
- 截距项不为0
- 数据序列无缺失

-
LM法适用于更多阶数的滞后

补救方法
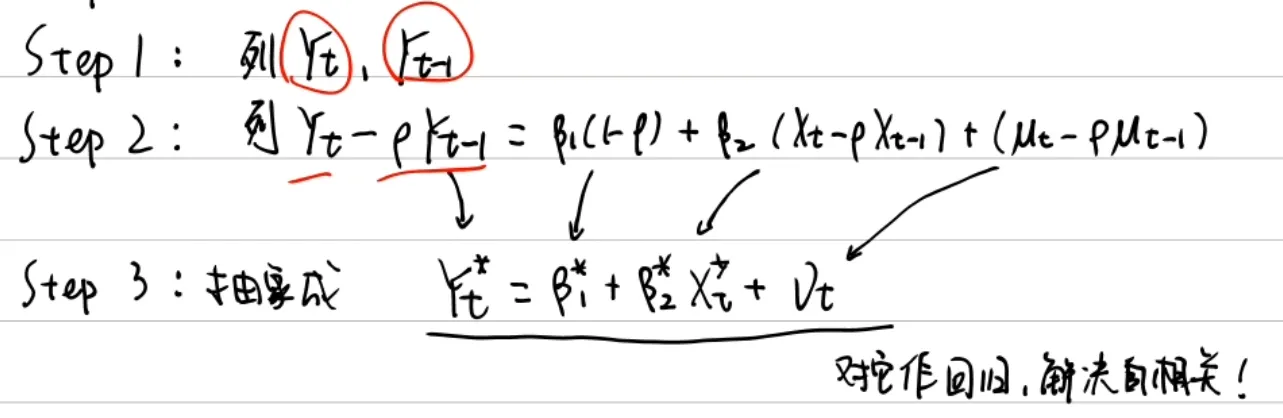
- 广义差分法

期末爆炸周,期末爆炸中