计量经济学 | 2. 线性回归模型

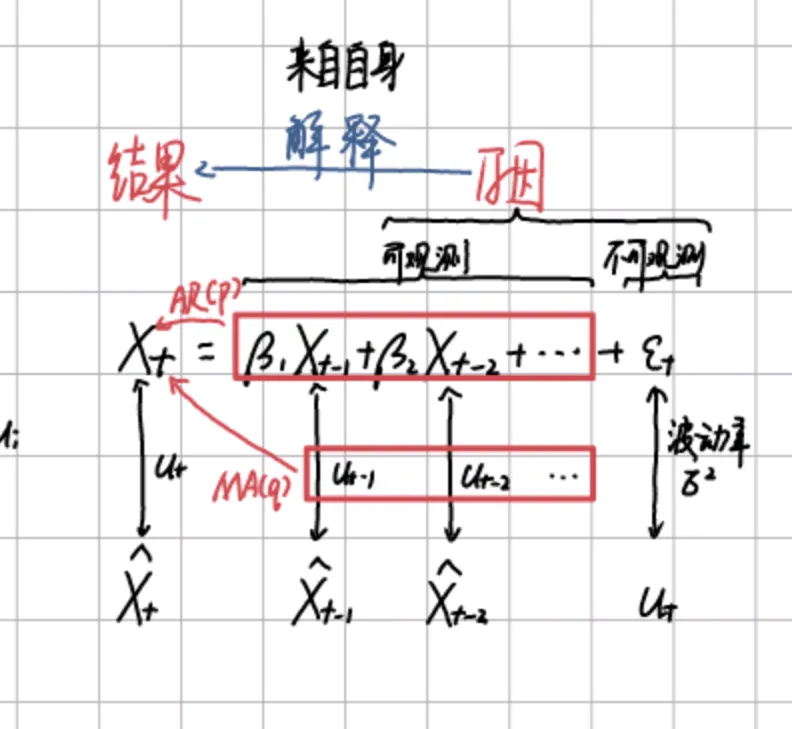
目录
[toc]

模型的设定

引例
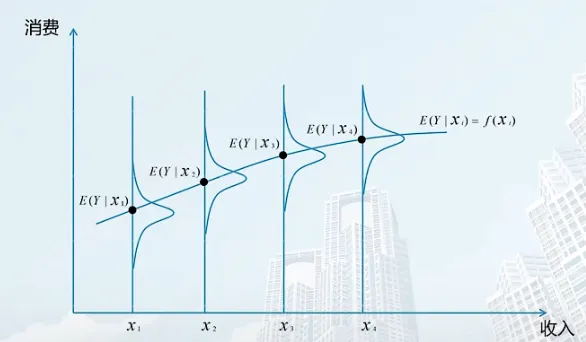
研究收入和消费的关系

在不同收入水平有消费的不同分布

总体回归方程

E(Y∣Xi)=f(Xi)E(Y|X_i)=f(X_i)

此方程代表总体Y的变化情况。如果将其写成一元线性形式，会得到：

总体线性方程

E(Y∣Xi)=f(Xi)=β0+β1∗Xi2E(Y|X_i)=f(X_i)=\beta_0+\beta_1 * X_i^2

系数的定义

  • β0\beta_0 截距项，即 xi=0x_i=0 时 E(Y∣Xi)E(Y|X_i) 的取值
  • β1\beta_1 斜率，即 xix_i 变化一个单位时，E(Y∣Xi)E(Y|X_i) 的变化

线性的定义
指的是系数的线性，而不是变量的线性

例一：

E(Y∣Xi)=f(Xi)=β0+β1∗Xi2E(Y|X_i)=f(X_i)=\beta_0+\beta_1 * X_i^2

此例系数是线性，而变量不是线性。但是我们可以把变量设定为Wi=Xi2W_i=X_i^2，此时方程就变为E(Y∣Xi)=f(Xi)=β0+β1∗Xi2=β0+β1∗WiE(Y|X_i)=f(X_i)=\beta_0+\beta_1 * X_i^2=\beta_0+\beta_1 * W_i

例二：

E(Y∣Xi)=f(Xi)=β0+(β1∗β0)∗Xi2E(Y|X_i)=f(X_i)=\beta_0+(\beta_1 * \beta_0) * X_i^2

此例子中，系数不是线性

注意：
回归方程表示总体Y的变化情况，但对于某个点，它不一定是条件期望（存在误差项）

误差项

ui=Yi−E(Y∣Xi)u_i=Y_i-E(Y|X_i)

其中 uiu_i 就是 误差项，是真实值 YiY_i 在某一确定的 XiX_i 下与期望值的偏离情况，又称为 随机扰动项

来源：

  • 理论模糊性
  • 变量的测量误差
  • 数据欠缺
  • 有意为之：简单性原则
  • 人类行为随机性
  • 错误方程形式

经典线性回归模型

我们已经知道，可以使用回归模型应用于计量经济的研究。回归模型中，最基础的是 简单线性回归模型(古典线性回归模型)。

简单线性回归模型是系数线性的模型。对它的基本假设有两个方面：

  • 一是对变量和模型的假定
  • 而是对随机扰动项 uiu_i 统计分布的假定

以下关于扰动项 uiu_i 的假设由高斯最早提出，又称为 高斯假定 或 古典假定。满足这样的假定的线性回归模型，又称为 古典线性回归模型

  • 假定一
    零均值假定，即随机扰动项的条件期望等于0，E(u∣x)=0E(u|x)=0 可以通俗理解为 x和u不相关
  • 假定二
    同方差假定，即对于每一个给定的 XiX_i，随机扰动项的条件方差都等于 σ2\sigma^2

Var(ui∣Xi)=E[ui−E(ui∣Xi)]2=E(ui2)=σ2Var(u_i\mid X_i)=E[u_i-E(u_i\mid X_i)]^2=E(u_i^2)=\sigma^2

  • 假定三
    无自相关假定，即各个扰动项的逐次值互不相关，也可以说他们的协方差等于零

Cov(ui,uj)=E[ui−E(ui)]E[uj−E(uj)]=0Cov(u_i, u_j)=E[u_i-E(u_i)]E[u_j-E(u_j)]=0

  • 假定四
    解释变量和扰动项不相关，协方差等于0

Cov(ui,Xi)=E[ui−E(ui)]E[Xi−E(Xi)]=0Cov(u_i, X_i)=E[u_i-E(u_i)]E[X_i-E(X_i)]=0

这一假定说明解释变量和扰动项是各自独立影响被解释变量的，从而得以分清各自的影响多少

  • 假定五
    正态性假定，即随机扰动项ui∼N(0,σ2)u_i\sim N(0, \sigma^2)

同时由上面的性质可以知道，Yi=β0+β1∗XiY_i=\beta_0+\beta_1 *X_i, YiY_i 的分布性质取决于 uiu_i, 因此对于于 YiY_i ，零均值、同方差、无自相关、正态性假定也都成立。

  • E(Yi∣Xi)=β0+β1XiE(Y_i|X_i)=\beta_0+\beta_1X_i
  • Var(Yi∣Xi)=E[Yi−E(Yi∣Xi)]2=E(Yi2)=σ2Var(Y_i\mid X_i)=E[Y_i-E(Y_i\mid X_i)]^2=E(Y_i^2)=\sigma^2
  • Cov(Yi,Yj)=E[Yi−E(Yi)]E[Yj−E(Yj)]=0Cov(Y_i, Y_j)=E[Y_i-E(Y_i)]E[Y_j-E(Y_j)]=0
  • Yi∼N(β0+β1Xi,σ2)Y_i\sim N(\beta_0+\beta_1X_i, \sigma^2)

实践中，假设4最容易被违反

例子：
u（残差）中包含能力，而能力与教育程度相关
income=β0+β1∗education+uincome = \beta_0 + \beta_1 * education +u

违反了假设4，u和x不是无关的

模型的估计

计量经济分析需要估计方程，原本 理论方程 为

Yi=β0+β1∗Xi+uiY_i=\beta_0 + \beta_1 * X_i + u_i

如果对方程进行估计，可以得到 估计方程 如下

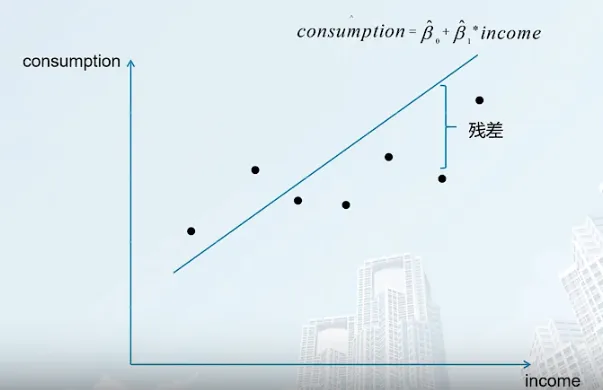
Yi^=β0^+β1^∗Xi\hat{Y_i}=\hat{\beta_0} + \hat{\beta_1} * X_i

此方程又称为 样本回归函数 (sample regression function, SRF)

数据（样本）

抽样调查：随机抽取1000个人
每个人都有一组收入和消费的数据

{consumptioni,incomei},i=1,...,1000\left\{consumption_i, income_i \right\}, i=1, ..., 1000

由于构建的回归直线无法通过每一个点，为了让回归直线拟合性更高，我们需要使用 最小二乘估计法OLS

最小二乘估计法OLS

选择 β0^\hat{\beta_0} 和 β1^\hat{\beta_1}使得残差 eie_i 的平方和最小

min⁡∑ei2=Min(β0^,β1^)∑i=1n(Yi−β0^−β1^∗Xi)2\min\sum e_i^2=\mathop{Min}\limits_{(\hat{\beta_0},\hat{\beta_1})}\sum_{i=1}^{n}(Y_i-\hat{\beta_0}-\hat{\beta_1}*X_i)^2

一阶条件

−Min(β0^,β1^)∑i=1n2⋅(Yi−β0^−β1^∗Xi)(1)-\mathop{Min}\limits_{(\hat{\beta_0},\hat{\beta_1})}\sum_{i=1}^{n}2\cdot(Y_i-\hat{\beta_0}-\hat{\beta_1}*X_i)\tag{1}

−Min(β0^,β1^)∑i=1n2Xi⋅(Yi−β0^−β1^∗Xi)(2)-\mathop{Min}\limits_{(\hat{\beta_0},\hat{\beta_1})}\sum_{i=1}^{n}2 X_i\cdot(Y_i-\hat{\beta_0}-\hat{\beta_1}*X_i)\tag{2}

解方程可以得出

β1^=∑i=1n(Xi−Xˉ)(Yi−Yˉ)∑i=1n(Xi−Xˉ)2=∑xiyi∑xi2(1)\hat{\beta_{1}}=\cfrac{\sum\limits_{i=1}^n(X_i-\bar{X})(Y_i-\bar{Y})}{\sum\limits_{i=1}^n(X_i-\bar{X})^2}=\cfrac{\sum x_iy_i}{\sum x_i^2} \tag{1}

β0^=Yˉ−β1^Xˉ(2)\hat{\beta_0}=\bar{Y}-\hat{\beta_1}\bar{X}\tag{2}

其中，
{Xˉ=1n∑i=1nXiYˉ=1n∑i=1nYi\begin{cases} \bar{X}=\cfrac{1}{n}\sum\limits_{i=1}^{n}X_i\\\bar{Y}=\cfrac{1}{n}\sum\limits_{i=1}^{n}Y_i \end{cases}

大写XiX_i, YiY_i表示观测值
小写xix_i, yiy_i表示离差

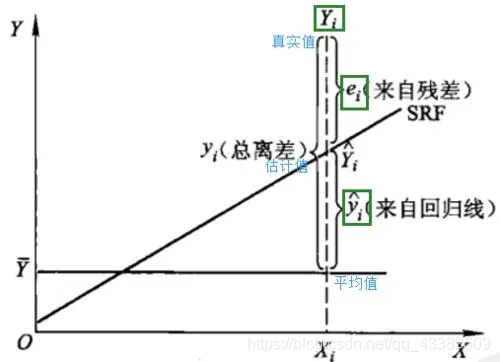
离差（Deviation）、残差（Residual）、回归差与误差（Error）

本部分摘抄自

离差（Deviation）

离差（Deviation） 实际上讲的是一种个体样本偏离总样本平均的程度，严谨的说法是实际观察值与其平均值的偏离程度。定义式为：

di=Yi−Yˉd_i=Y_i-\bar{Y}

其中 Yˉ=1n∑n=1nYi\bar{Y}=\frac{1}{n}\sum\limits_{n=1}^n Y_i

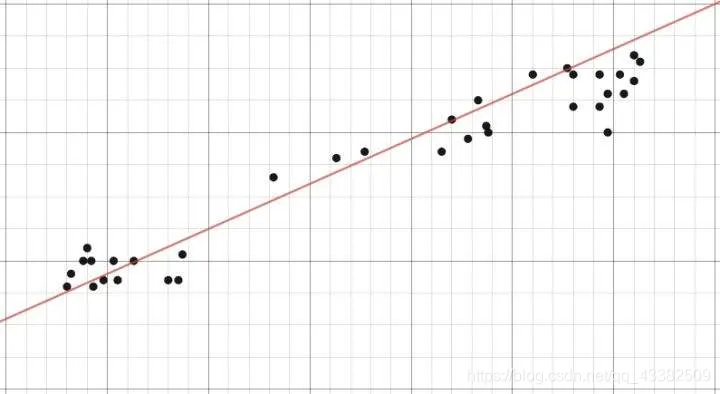
图1 样本散点图与样本均值线（图中红线为样本均值线，黑点为样本真实值。真实值与样本均值线的差即为离差）

需要特别注意的是，离差只与样本有关，而与模型总体无关——它只是衡量样本因变量与其平均值的差。

就像当代著名散文家—沃兹几所言：“不论模型是什么，离差都在那里。如果你愿化作样本，那么离差就是你与那样本海洋之中灯塔的距离。”

如果我们对被解释变量 YiY_i 的离差 yiy_i 进行加总，可以得到

∑n=1nyi (total sum of squares, TSS)\sum\limits_{n=1}^n y_i\ \text{(total sum of squares, TSS)}

残差（Residual）

残差（Residual）这个“残”字其实已经把这个意思说的明白了。在新华字典中，“残”的意思就是“剩下的”。让我们想想，在多元回归拟合过程中，什么东西是“剩下”的呢？对了！就是在使用样本估计总体后，因变量真值在被模型拟合完后还剩下的、没有放入模型的那一部分差值。用百度官方的说法，就是实际观察值与估计值（拟合值）之间的差。定义式为：

ei=Yi−Y^e_i=Y_i-\hat{Y}

样本散点图与拟合线（图中红线为拟合曲线，黑点为样本真实值。真实值与样本拟合值的差即为残差。

如果我们对被解释变量 YiY_i 的残差进行加总，可以得到

∑n=1nei (residual sum of squares, RSS)\sum\limits_{n=1}^{n}e_i\ \text{(residual sum of squares, RSS)}

回归差

回归差是散点图中被解释变量拟合值 Yi^\hat{Y_i} 和其均值 Yˉ\bar{Y} 之差，定义式为

Yi^−Yˉ\hat{Y_i}-\bar{Y}

如果对回归差进行加总，可以得到

∑n=1n(Yi^−Yˉ) (explained sum of squares, ESS)\sum\limits_{n=1}^n(\hat{Y_i}-\bar{Y}) \ \text{(explained sum of squares, ESS)}

误差（Error）

误差（Error） 又称随机扰动项 uu，英文本意就是“错误”。我们在日常生活中总是会犯这样或那样的错误，模型其实就是简化了的现实世界，其也必然会包含错误。而在多元回归模型中，我们在建立模型的时候就已经加入了这个错误：误差项。比如，在多元回归模型：

Yi=β0+β1∗Xi+εY_i=\beta_0 + \beta_1 * X_i + \varepsilon

其中的 ϵ\epsilon 就是误差

另一个角度来看，可以认为随机扰动项 u=Yi−E(Y∣xi)u=Y_i-E(Y\mid x_i)

因此，我们所谓的“误差”本质上是一个随机变量——它是衡量模型总体性质的一个指标，是总体性质的体现，而与样本无关。

正如唐代著名诗人—鲁迅（Shuren Zhou） 在《吾未曾曰过》中所言：“不论抽样与否，误差都在那里，不增不减、不舍不弃。”

关系


容易看出，总离差可分解为残差与拟合值两部分，也可以认为离差被分解为了残差与回归差两部分。因此，残差可以视为离差的一个来源。

正如上文所言，我们把总离差的加和命名为 TSSTSS，残差加和命名为 RSSRSS，回归差加和命名为 RSSRSS，根据总离差的分解，可以得出以下等式：

TSS=RSS+ESSTSS=RSS+ESS

对于误差和残差而言，
εi=Yi−f(Xi)\varepsilon_i=Y_i-f(X_i)
ei=Yi−f(Xi)^e_i=Y_i-\widehat{f(X_i)}
从定义式来看，二者长得十分相似：都是因变量 Y 与模型 f (X) 的偏差。二者的不同之处是：误差描述了总体的性质，而残差描述了样本点的性质。因此，残差 eie_i 其实是误差 εiε_i 的一个“抽样”，或者说是一个估计值。

OLS回归线的性质

基本性质

拟合值 Yi^=β0^+β1^∗Xi\hat{Y_i}=\hat{\beta_0}+\hat{\beta_1}*X_i

残差（代表真实值和拟合值之间的差距） ei=Yi−Yi^e_i=Y_i-\hat{Y_i}

使用普通最小二乘法拟合的样本回归线有以下性质：

  1. 所拟合的直线一定通过x和y的均值点
    Yˉ=β^0+β^1Xˉ\bar{Y}=\hat{\beta}_0+\hat{\beta}_1\bar{X}

  2. 估计量的均值等于实际值的均值

  3. 剩余项 eie_i 的均值等于0

  4. 被解释变量和剩余项 eie_i 不相关

  5. 解释变量和剩余项 eie_i 不相关

OLS估计量的统计性质

参数估计量评价标准

无偏性

E(β0^∣x)=β0E(\hat{\beta_0}|x)=\beta_0

E(β1^∣x)=β1E(\hat{\beta_1}|x)=\beta_1

注意：
无偏性正确理解为：每次抽样可以理解为一个估计值，抽样次数趋于无穷，估计值的均值趋于真实值。无偏性不代表每个一次抽样的估计值所估计出的系数等于真实值。

有效性

有效性是指，估计量应具有最小方差性， Varβ^≤Varβ^Var{\hat{\beta}}\le Var\hat{\beta}

一致性

样本太少时很难得到无偏估计量，所有应当考虑容量充分大或趋于无穷大时估计量的渐进性质。

由切比雪夫不等式，当n趋于无穷，有

lim⁡n→∞P(∣β^−β∣)<ϵ=1\lim\limits_{n\to \infty}P(\mid\hat{\beta}-\beta\mid)<\epsilon=1

此时称其为一致估计量

估计量的统计特性

线性

线性是指：系数与被解释变量之间线性，也就是β^0\hat{\beta}_0, β^1\hat{\beta}_1 与 YiY_i 线性。

无偏性

E(β0^)=β0E(\hat{\beta_0})=\beta_0
E(β1^)=β1E(\hat{\beta_1})=\beta_1

有效性

在同方差 var(ui∣Xi)=E(ui2)=σ2var(u_i\mid X_i)=E(u_i^2)=\sigma^2 和无自相关 Cov(ui,uj)=E(ui,uj)=0Cov(u_i, u_j)=E(u_i, u_j)=0 假定成立时，有

Var(β^1)=σ2∑xi2Var({\hat\beta}_1)=\cfrac{\sigma^2}{\sum x_i^2}

Var(β^0)=σ2∑Xi2n∑xi2Var({\hat\beta}_0)=\sigma^2\cfrac{\sum X_i^2}{n\sum x_i^2}

由此可知，普通最小二乘得到的系数具有最小方差性。

计量经济学还可以用标准误差 度量估计量的精准性
SE(β^2)=σ∑xi2SE({\hat\beta_2})=\cfrac{\sigma}{\sqrt{\sum x_i^2}}

SE(β^2)=σ∑Xi2n∑xi2SE({\hat\beta_2})=\sigma\sqrt{\cfrac{\sum X_i^2}{n\sum x_i^2}}

一般而言，方差σ\sigma难以得知，常用 σ2=∑ei2n−2\sigma^2=\cfrac{\sum e_i^2}{n-2} 作为方差的无偏估计，∑ei2\sum e_i^2 是剩余平方和， n−2n-2 是自由度。

综上所述，古典假定条件下，OLS估计量 是参数的 最佳线性无偏估计量 (best linear unbiased estimator, Blue)，也因此可以得到最小的置信区间。

波动程度

对离差进行分解，可以得出

Yi=Yi^+eiY_i=\hat{Y_i}+e_i

(Yi−Yiˉ)=(Yi^−Yˉ)+ei(Y_i-\bar{Y_i})=(\hat{Y_i}-\bar{Y})+e_i

进而得出

∑Yi2=∑Y^i+∑ei2\sum Y_i^2=\sum\hat{Y}_i+\sum e_i^2

用OLS估计由此可得出三条性质

∑i=1nui^=0(1)\sum\limits_{i=1}^{n}\hat{u_i}=0 \tag{1}

∑i=1nui^⋅xi=0(2)\sum\limits_{i=1}^{n}\hat{u_i} \cdot x_i=0 \tag{2}

∑i=1nyi^⋅ui^=0(3)\sum\limits_{i=1}^{n}\hat{y_i} \cdot \hat{u_i}=0 \tag{3}

因此可以得出：

  • Total sum of squares (TSS)
    TSS=∑i=1n(yi−yˉ)2TSS=\sum\limits_{i=1}^{n}(y_i-\bar{y})^2
    散点图各点到均值的和，表示 真实值 YiY_i 的波动程度，是总离差加和
  • Explained sum of squares (ESS)
    ESS=∑i=1n(yi^−y^ˉ)2,yˉ=y^ˉESS=\sum\limits_{i=1}^{n}(\hat{y_i}-\bar{\hat{y}})^{2}, \bar{y}=\bar{\hat{y}}
    回归方程线上各点到均值的和，表示 拟合值 Yˉi\bar{Y}_i 波动程度，是回归差的加和
  • Residual sum of squares (RSS)
    RSS=∑i=1nu^i2RSS=\sum\limits_{i=1}^{n}\hat{u}_i^2
    散点图各点到回归方程同一横坐标各点的和距离之和，表示 残差 eie_i 波动程度，是残差的加和
  • 关系

TSS=ESS+RSSTSS=ESS+RSS

真实值波动程度等于残差的波动程度加上拟合值波动程度

拟合优度、可决系数

概念和性质

拟合优度 R-squared

拟合优度是判断拟合性质的标准，可以用如下 可决系数 这一指标进行度量：

R2=ESSTSS=1−RSSTSS=∑i=1n(Yi^−Yˉ)2∑i=1n(Yi−Yˉ)2=∑i=1nyi^2∑i=1nyi2R^2=\cfrac{ESS}{TSS}=1-\cfrac{RSS}{TSS}=\cfrac{\sum\limits_{i=1}^{n}(\hat{Y_i}-\bar{Y})^{2}}{\sum\limits_{i=1}^{n}(Y_i-\bar{Y})^2}=\cfrac{\sum\limits_{i=1}^{n}\hat{y_i}^2}{\sum\limits_{i=1}^{n}y_i^2}

被解释变量中能够由解释变量解释的百分比，或者说是拟合值波动程度与真实值的波动程度之比。

例如：
经过计算，某抽样实验的可决系数等于 99.39%99.39\%，代表此样本被解释变量观测值的总变差中，有 99.39%99.39\% 由所估计的样本回归模型做出了解释。

可决系数的特点如下：

  • 非负性
  • 取值范围 0≤R2≤10\le R^2\le 1
  • 可决系数是样本观测值的函数，是随抽样变动的随机变量

注意
使用不同抽样的样本，所得到的估计值是不同的。通常人们只做一次抽样，如何通过 估计的系数值 推断 系数的真实性？统计中，由估计值来推断真实值的做法叫做 统计推断 。为了做统计推断，需要引入一系列结社。下面介绍 经典 （又称为高斯或标准）线性回归模型的主要假设

可决系数R2R^2和相关系数rr

在一元线性回归模型中，可决系数R2R^2是相关系数rr的平方，r=±R2r=\pm\sqrt{R^2}

虽然二者在数值上一致，但是代表的意义截然不同：

  • 可决系数是度量回归模型对被解释变量变差的结实程度，取值范围是 0 到 1
  • 相关系数是就两个变量而言，说明两个变量的线性依存程度，取值范围是 -1 到 +1

回归系数的假设检验和区间估计

OLS估计的分布性质

在古典假设下，随机扰动项服从正态分布，为此YiY_i也服从正态分布。

对于系数而言：

  • 在大样本情况下，YiY_i即使不服从正态分布，β1^\hat{\beta_1}、β2^\hat{\beta_2}也会趋于正态分布。

  • 在小样本情况下，同时我们知道，β1^\hat{\beta_1}、β2^\hat{\beta_2}是YiY_i的线性函数，因此他们也服从正态分布。

β1^∼N(β1,σ2∑Xi2n∑xi2)\hat{\beta_1}\sim N(\beta_1, \sigma^2\cfrac{\sum X_i^2}{n\sum x_i^2})

β2^∼N(β2,σ2∑xi2)\hat{\beta_2}\sim N(\beta_2, \cfrac{\sigma^2}{\sum x_i^2})

对他们进行标准化，可以得到：

z1=β1^−β1σ2∑Xi2n∑xi2=β1^−β1SE(β^1)∼N(0,1)z_1=\cfrac{\hat{\beta_1}-\beta_1}{\sqrt{\sigma^2\cfrac{\sum X_i^2}{n\sum x_i^2}}}=\cfrac{\hat{\beta_1}-\beta_1}{SE(\hat{\beta}_1)}\sim N(0,1)

z2=β2^−β2σ2∑xi2=β2^−β2SE(β^2)∼N(0,1)z_2=\cfrac{\hat{\beta_2}-\beta_2}{\sqrt{\cfrac{\sigma^2}{\sum x_i^2}}}=\cfrac{\hat{\beta_2}-\beta_2}{SE(\hat{\beta}_2)}\sim N(0,1)

但是由于我们难以得知σ\sigma，常用它的无偏估计代替。

  • 大样本情况下，使用无偏估计 σ^2=∑ei2n−2\hat{\sigma}^2=\cfrac{\sum e_i^2}{n-2}去代替 σ2\sigma^2 ，此时用估计的标准误差作β^1\hat{\beta}_1、β^2\hat{\beta}_2的标准化变换得到的z1z_1、z2z_2，仍可以视为标准正态分布变量
  • 小样本情况下，用无偏估计σ^2\hat{\sigma}^2会得到SE^(β^1)\widehat{SE}(\hat{\beta}_1)、SE^(β^2)\widehat{SE}(\hat{\beta}_2)并由此作标准化变换得到的z1z_1、z2z_2服从的不是正态分布而是自由度为2的t分布，设此时变换值为t，则

t1=β^1−β1SE^(β^1)=β1^−β1σ^2∑Xi2n∑xi2∼t(n−2)t_1=\cfrac{\hat{\beta}_1-\beta_1}{\widehat{SE}(\hat{\beta}_1)}=\cfrac{\hat{\beta_1}-\beta_1}{\sqrt{\hat{\sigma}^2\cfrac{\sum X_i^2}{n\sum x_i^2}}}\sim t(n-2)

t2=β^2−β2SE^(β^2)=β2^−β2σ^2n∑xi2∼t(n−2)t_2=\cfrac{\hat{\beta}_2-\beta_2}{\widehat{SE}(\hat{\beta}_2)}=\cfrac{\hat{\beta_2}-\beta_2}{\sqrt{\cfrac{\hat{\sigma}^2}{n\sum x_i^2}}}\sim t(n-2)

回归系数的假设检验

根据参数假设检验的不同要求，会作不同的假设

  • H0:β2=β2∗H_0: \beta_2=\beta_2^*，H1:β2≠β2∗H_1: \beta_2\neq \beta_2^*
  • H0:β2≥β2∗H_0: \beta_2\ge\beta_2^*，H1:β2<β2∗H_1: \beta_2<\beta_2^*
  • H0:β2≤β2∗H_0: \beta_2\le\beta_2^*，H1:β2>β2∗H_1: \beta_2>\beta_2^*

因此，会进行不同的假设检验

  • 单侧检验
    • H0:β2=β2∗H_0: \beta_2=\beta_2^*，H1:β2≠β2∗H_1: \beta_2\neq \beta_2^*
  • 双侧检验
    • H0:β2≥β2∗H_0: \beta_2\ge\beta_2^*，H1:β2<β2∗H_1: \beta_2<\beta_2^*
    • H0:β2≤β2∗H_0: \beta_2\le\beta_2^*，H1:β2>β2∗H_1: \beta_2>\beta_2^*

检验方法主要有：Z检验（σ2已知\sigma^2已知）、t检验（σ2未知\sigma^2未知）

Z检验

在σ2\sigma^2已知的情况下，对于给定的显著性水平（置信水平）α\alpha，可以写出

P{当H0为真时拒绝H1}≤αP\left\{当H_0为真时拒绝H_1\right\}\le \alpha

由正态分布的性质，可以得出

P{当H0为真时拒绝H1}=Pμ0{∣Xˉ−μ0σ/n∣≥k}=αP\left\{当H_0为真时拒绝H_1\right\}=P_{\mu_0}\left\{\left\vert \cfrac{\bar{X}-\mu_0}{\sigma/\sqrt{n}} \right\vert\ge k\right\} =\alpha

此时，在正态分布的图像上，大于的点应当是 zα/2z_{\alpha/2}

因此，如果∣z∣=∣Xˉ−μ0σ/n∣≥k=zα/2\left\vert z \right\vert=\left\vert \cfrac{\bar{X}-\mu_0}{\sigma/\sqrt{n}} \right\vert\ge k=z_{\alpha/2}

那么就拒绝原假设，反之接受

对于单侧检验(大于或小于)，依据我们设定的对立假设写出置信区间，如果符合对立假设就拒绝原，反之就接受原假设

由此可得出

原假设 对立假设 构造统计量 置信区间
H0:β2=β2∗H_0: \beta_2=\beta_2^* H1:β2≠β2∗H_1: \beta_2\neq \beta_2^* ∣z∣=∣β2^−β2SE(β^2)∣\left\vert z \right\vert=\left\vert \cfrac{\hat{\beta_2}-\beta_2}{SE(\hat{\beta}_2)} \right\vert ∣z∣≥zα/2\left\vert z \right\vert\ge z_{\alpha/2}
H0:β2≥β2∗H_0: \beta_2\ge\beta_2^* H1:β2<β2∗H_1: \beta_2<\beta_2^* $ z = \cfrac{\hat{\beta_2}-\beta_2}{SE(\hat{\beta}_2)} $ $ z \le - z_{\alpha}$
H0:β2≤β2∗H_0: \beta_2\le\beta_2^* H1:β2>β2∗H_1: \beta_2>\beta_2^* $ z = \cfrac{\hat{\beta_2}-\beta_2}{SE(\hat{\beta}_2)} $ $ z \ge z_{\alpha}$

t检验

当我们无法得知σ2\sigma^2时，我们选择使用t检验（因为我们使用无偏估计量去替代原σ2\sigma^2，导致此时统计量不再符合正态分布，而是 符合自由度为2的t分布）
σ^2=∑ei2n−2\hat{\sigma}^2=\cfrac{\sum e_i^2}{n-2}

因此，上面的表格就会变成

原假设 对立假设 构造统计量 置信区间
H0:β2=β2∗H_0: \beta_2=\beta_2^* H1:β2≠β2∗H_1: \beta_2\neq \beta_2^* ∣t∣=∣β2^−β2SE^(β^2)∣\left\vert t \right\vert=\left\vert \cfrac{\hat{\beta_2}-\beta_2}{\widehat{SE}(\hat{\beta}_2)} \right\vert ∣t∣≥tα/2(n−2)\left\vert t \right\vert\ge t_{\alpha/2}(n-2)
H0:β2≥β2∗H_0: \beta_2\ge\beta_2^* H1:β2<β2∗H_1: \beta_2<\beta_2^* $ t = \cfrac{\hat{\beta_2}-\beta_2}{\widehat{SE}(\hat{\beta}_2)} $ $ t \le - t_{\alpha}(n-2)$
H0:β2≤β2∗H_0: \beta_2\le\beta_2^* H1:β2>β2∗H_1: \beta_2>\beta_2^* $ t = \cfrac{\hat{\beta_2}-\beta_2}{\widehat{SE}(\hat{\beta}_2)} $ $ t \ge t_{\alpha}(n-2)$

回归系数的区间估计

β1^∼N(β1,σ2∑Xi2n∑xi2)\hat{\beta_1}\sim N(\beta_1, \sigma^2\cfrac{\sum X_i^2}{n\sum x_i^2})
β2^∼N(β2,σ2∑xi2)\hat{\beta_2}\sim N(\beta_2, \cfrac{\sigma^2}{\sum x_i^2})

t1=β^1−β1SE^(β^1)=β1^−β1σ^2∑Xi2n∑xi2∼t(n−2)t_1=\cfrac{\hat{\beta}_1-\beta_1}{\widehat{SE}(\hat{\beta}_1)}=\cfrac{\hat{\beta_1}-\beta_1}{\sqrt{\hat{\sigma}^2\cfrac{\sum X_i^2}{n\sum x_i^2}}}\sim t(n-2)
t2=β^2−β2SE^(β^2)=β2^−β2σ^2∑xi2∼t(n−2)t_2=\cfrac{\hat{\beta}_2-\beta_2}{\widehat{SE}(\hat{\beta}_2)}=\cfrac{\hat{\beta_2}-\beta_2}{\sqrt{\cfrac{\hat{\sigma}^2}{\sum x_i^2}}}\sim t(n-2)

区间估计 实质是根据置信度 1−α1-\alpha 以及统计量的分布情况（正态分布、t分布等），写出左右两个临界值使得临界值中间的区域的概率是1−α1-\alpha，化简得到的就是统计量的置信区间，表示统计量落在这个范围的估计是可信的。

P(β^2−δ≤β2≤β^2+δ)=1−αP(\hat{\beta}_2-\delta\le \beta_2\le\hat{\beta}_2+\delta)=1-\alpha

以 正态分布 为例：
在总体方差σ2\sigma^2已知的情况下，由于置信度是 1−α1-\alpha ，根据正态分布的概率密度函数，可以知道左右两个临界值分别是 −Zα/2-Z_{\alpha/2} 、Zα/2Z_{\alpha/2}

P(−Zα/2≤Z∗≤Zα/2)=1−αP(-Z_{\alpha/2}\le Z^* \le Z_{\alpha/2})=1-\alpha

总体方差未知的情况下，当样本量充分大时，我们使用无偏估计σ^2=∑ei2n−2\hat{\sigma}^2=\cfrac{\sum e_i^2}{n-2}去代替，此时仍然可以认为它符合正态分布，可以得到

P(−Zα/2≤Z∗≤Zα/2)=1−αP(-Z_{\alpha/2}\le Z^* \le Z_{\alpha/2})=1-\alpha

但是，在总体方差未知、样本量较小时，此时不可以认为估计量得到的依然是正态分布，而应当是做自由度为2的t分布。

t2=β^2−β2SE^(β^2)=β2^−β2σ^2∑xi2∼t(n−2)t_2=\cfrac{\hat{\beta}_2-\beta_2}{\widehat{SE}(\hat{\beta}_2)}=\cfrac{\hat{\beta_2}-\beta_2}{\sqrt{\cfrac{\hat{\sigma}^2}{\sum x_i^2}}}\sim t(n-2)

P(−tα/2(n−2)≤t∗≤tα/2(n−2))=1−αP(-t_{\alpha/2}(n-2)\le t^* \le t_{\alpha/2}(n-2))=1-\alpha

P[β^2−tα/2SE^(β^2)≤β2≤β^2+tα/2SE^(β^2)]=1−αP\left[ \hat{\beta}_2-t_{\alpha/2 }\widehat{SE}(\hat{\beta}_2)\le \beta_2 \le \hat{\beta}_2+t_{\alpha/2 }\widehat{SE}(\hat{\beta}_2) \right]=1-\alpha

回归模型的预测

对回归模型被解释变量的预测可以分为两大类：一类是平均值预测，一类是个别值预测。对于第一类平均值预测又可以分为点预测和区间预测。预测的方法和前文介绍的点估计、区间估计的方法类似，预测的基本依据正是此前提到的样本估计方程 Y^f=β^1+β^2Xf\hat{Y}_f=\hat{\beta}_1+\hat{\beta}_2X_f。但是由于此时统计量的不同，会导致一些细微的变化。

平均值预测

点预测

点预测的方法就是把需要的XfX_f带入样本回归函数Y^f=β^1+β^2Xf\hat{Y}_f=\hat{\beta}_1+\hat{\beta}_2X_f，求得的Y^f\hat{Y}_f就是我们需要的点预测值。

区间预测

区间预测的方法类似于求置信区间。此时我们需要对Y^f\hat{Y}_f构造统计量。根据分析可以知道：

E(Y^f)=E(Yf∣Xf)=β1+β2XfE(\hat{Y}_f)=E(Y_f\mid X_f)=\beta_1+\beta_2X_f

var(Yf^)=σ2[1n+(Xf−Xˉ)2∑xi2]var(\hat{Y_f})=\sigma^2\left[ \cfrac{1}{n}+\cfrac{(X_f-\bar{X})^2}{\sum x^2_i} \right]

SE(Yf^)=σ1n+(Xf−Xˉ)2∑xi2SE(\hat{Y_f})=\sigma \sqrt{ \cfrac{1}{n}+\cfrac{(X_f-\bar{X})^2}{\sum x^2_i} }

一般情况下σ2\sigma^2未知，用他的无偏估计∑ei2n−2\sum \cfrac{e^2_i}{n-2}代替，经过标准化构造出的统计量服从t分布

t=Yf^−E(Yf^)SE^(Yf^)=Yf^−E(Yf∣Xf)σ^1n+(Xf−Xˉ)2∑xi2∼t(n−2)t=\cfrac{\hat{Y_f}-E(\hat{Y_f})}{\widehat{SE}(\hat{Y_f})}=\cfrac{\hat{Y_f}-E(Y_f\mid X_f)}{\hat{\sigma} \sqrt{ \cfrac{1}{n}+\cfrac{(X_f-\bar{X})^2}{\sum x^2_i}}} \sim t(n-2)

根据给定的置信水平α\alpha

P{−tα/2≤t∗≤tα/2}P\left\{ -t_{\alpha/2} \le t^* \le t_{\alpha/2} \right\}

可以得到置信区间

[(Yf^−tα/2SE(Yf^)),(Yf^+tα/2SE(Yf^))]\left[ \left( \hat{Y_f}-t_{\alpha/2 }SE(\hat{Y_f}) \right), \left( \hat{Y_f}+t_{\alpha/2 }SE(\hat{Y_f}) \right) \right]

个别值预测

基本方法和上文的区间预测一致。在此处，我们需要对YfY_f进行预测，就必须要知道残差efe_f相关性质
E(ef)=0E(e_f)=0
Var(ef)=σ2[1+1n+(Xf−Xˉ)2∑xi2]Var(e_f)=\sigma^2\left[ 1+\cfrac{1}{n}+\cfrac{(X_f-\bar{X})^2}{\sum x^2_i} \right]

由此构造出t统计量，根据置信水平，写出置信区间，化简之后得到：

[(Yf^−tα/2SE(ef^)),(Yf^+tα/2SE(ef^))]\left[ \left( \hat{Y_f}-t_{\alpha/2 }SE(\hat{e_f}) \right), \left( \hat{Y_f}+t_{\alpha/2 }SE(\hat{e_f}) \right) \right]

据此，可以看出平均值预测和个别值预测的特点：

  • 由于抽样误差的存在，可以看出个别值波动情况更大，因此预测区间更宽
  • 对YfY_f的平均值、个别值预测区间都不是常数，而是随解释变量XfX_f变化而变化。当Xˉ\bar{X}和XfX_f距离越近，精度越高，区间越窄；反之精度越低，区间越宽。所以应当注意XfX_f的取值。
  • 预测区间和样本容量有关。n越大，区间越窄，方差越小，精度越高。（大数定律）

线性回归模型的应用案例

基本步骤：

  • 明确目的和要求
  • 设定模型
    • 做出图形
    • 建立模型
  • 估计参数
  • 模型检验
    • 经济意义
    • 拟合优度R2R^2
    • 统计检验(t检验)
  • 回归预测