目录
[toc]

模型的设定和估计

为什么用 多元线性回归 ？
因为一元线性回归的结果很难建立因果关系

引例：
income^=0.5+700∗schoolingyear\hat{income}=0.5+700*schoolingyear

样本中可看出多一年教育年限收入就多700元，但我们不能简单得出 “增加一年教育年限，收入就可以提高700元” 的结论

多元回归 可以通过增加更多变量改善因果关系的建立

income^=0.5+700∗schoolingyear+500∗age\hat{income}=0.5+700*schoolingyear + 500*age

这个式子说明，年龄一样的人，教育年限多一年，收入平均多700元。如果我们通过控制所有特征（保证单一变量），得出的系数就可以认为是 建立起了教育年限和收入的因果关系

当然，由于我们不可能控制所有变量，多元回归分析只能说是改善而不是完全解决一元回归存在的问题

多元估计的一般形式

y=β0+β1∗x1+β2∗x2+⋯+βk∗xk+uy=\beta_0+\beta_1 * x_1+\beta_2 * x_2 + \cdots + \beta_k*x_k+u

多元估计的矩阵形式

如果对被解释变量做n次观测，得到的n组观测值的线性关系，实际上可以写成矩阵形式：

[Y1Y2⋮Ym]=[1X21X31⋯Xn11X22X32⋯Xn2⋮⋮⋮⋮1X2mX3m⋯Xnm][β1β2⋮βm]+[u1u2⋮um]\begin{bmatrix} Y_1\\ Y_2 \\ \vdots \\ Y_m \end{bmatrix}= \begin{bmatrix} 1 & X_{21} & X_{31} & \cdots & X_{n1}\\ 1 & X_{22} & X_{32} & \cdots & X_{n2}\\ \vdots & \vdots & \vdots & & \vdots & \\ 1 & X_{2m} & X_{3m} & \cdots & X_{nm}\\ \end{bmatrix} \begin{bmatrix} \beta_1 \\ \beta_2 \\ \vdots \\ \beta_m \\ \end{bmatrix}+ \begin{bmatrix} u_1 \\ u_2 \\ \vdots \\ u_m \\ \end{bmatrix}

多元总体线性回归函数的矩阵形式：

Y=Xβ+UY=X\beta+U

E(Y)=XβE(Y)=X\beta

类似的，我们可以把多元样本线性回归函数写成

Y=Xβ^+eY=X \hat{\beta}+e

Y^=Xβ^\hat{Y}=X\hat{\beta}

简单线性回归基本假定

  • 假定一
    零均值假定，即随机扰动项的条件期望等于0
  • 假定二
    同方差假定，即对于每一个给定的 XiX_i，随机扰动项的条件方差都等于 σ2\sigma^2

Var(ui∣Xi)=E[ui−E(ui∣Xi)]2=E(ui2)=σ2Var(u_i\mid X_i)=E[u_i-E(u_i\mid X_i)]^2=E(u_i^2)=\sigma^2

  • 假定三
    无自相关假定，即各个扰动项的逐次值互不相关，也可以说他们的协方差等于零

Cov(ui,uk)=E[ui−E(ui)]E[uk−E(uk)]={σ2,i=k0,i≠k(i,k=1,2,3,⋯n)\begin{aligned} Cov(u_i, u_k)&=E[u_i-E(u_i)]E[u_k-E(u_k)]\\ &=\begin{cases} \sigma^2, &i=k \\ 0, &i\neq k \end{cases} &(i, k=1,2,3,\cdots n) \end{aligned}

也就是说，

Var(U)=[σ20⋯00σ2⋯0⋮⋮⋱⋮00⋯σ2]=σ2InVar(U)=\begin{bmatrix} \sigma^2 & 0 & \cdots & 0 \\ 0 & \sigma^2 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & \sigma^2 \end{bmatrix}=\sigma^2I_n

  • 假定四
    解释变量和扰动项不相关，协方差等于0

Cov(ui,Xi)=E[ui−E(ui)]E[Xi−E(Xi)]=0Cov(u_i, X_i)=E[u_i-E(u_i)]E[X_i-E(X_i)]=0

这一假定说明解释变量和扰动项是各自独立影响被解释变量的，从而得以分清各自的影响多少

  • 假定五
    正态性假定，即随机扰动项ui∼N(0,σ2)u_i\sim N(0,\sigma^2)
  • 假定六
    无多重共线性。假设各解释变量的观测值线性无关，此时矩阵XX满秩，也就是Rank(X)=k\text{Rank}(X)=k，方阵XTXX^TX满秩，从而方阵XTXX^TX可逆

最小二乘估计

OLS残差平方和最小

Min∑ei2=Min{β^0,β^1,⋯ ,β^k}∑i=1n(Yi−β^0−β^1⋅Xi1−⋯−β^k⋅Xik)\mathop{Min}\sum e_{i}^2=\mathop{Min}\limits_{\left\{\hat{\beta}_0, \hat{\beta}_1, \cdots, \hat{\beta}_k\right\}}\sum\limits_{i=1}^{n}(Y_i-\hat{\beta}_0-\hat{\beta}_1 \cdot X_{i1}- \cdots -\hat{\beta}_k \cdot X_{ik})

需要

∂(∑ei2)∂β^j=0,(j=1,2,⋯ ,k)\cfrac{\partial(\sum e_{i}^2)}{\partial\hat{\beta}_j}=0, (j=1, 2, \cdots , k)

即

−∑i=1n2⋅(Yi−β0^−β^1⋅Xi1−⋯−β^k⋅Xik)=0−∑i=1n2⋅Xi1⋅(Yi−β0^−β^1⋅Xi1−⋯−β^k⋅Xik)=0⋮−∑i=1n2⋅Xik⋅(Yi−β0^−β^1⋅Xi1−⋯−β^k⋅Xik)=0\begin{aligned} &-\sum\limits_{i=1}^{n}2 \cdot (Y_i-\hat{\beta_0}-\hat{\beta}_1 \cdot X_{i1}-\cdots-\hat{\beta}_k \cdot X_{ik})=0 \\ &-\sum\limits_{i=1}^{n}2 \cdot X_{i1} \cdot (Y_i-\hat{\beta_0}-\hat{\beta}_1 \cdot X_{i1}-\cdots-\hat{\beta}_k \cdot X_{ik})=0 \\ &\vdots \\ &-\sum\limits_{i=1}^{n}2 \cdot X_{ik} \cdot (Y_i-\hat{\beta_0}-\hat{\beta}_1 \cdot X_{i1}-\cdots-\hat{\beta}_k \cdot X_{ik})=0\end{aligned}

括号中的正是残差efe_f，所以可以写出如下矩阵形式：

[∑ei∑X2iei⋮∑Xkiei]=XTe=[00⋮0]\begin{bmatrix} \sum e_i \\ \sum X_{2i}e_i \\ \vdots \\ \sum X_{ki}e_i \end{bmatrix}=X^Te= \begin{bmatrix} 0 \\ 0 \\ \vdots \\ 0 \end{bmatrix}

对多元回归方程左乘XTX^T

XTY=XTXβ^+XTe=XTXβ^\begin{aligned} X^TY&=X^TX \hat{\beta}+X^Te \\ &=X^TX \hat{\beta} \end{aligned}

由无多重共线性可知，XTXX^TX的逆矩阵存在，可以得出

β^=(XTX)−1XTY\hat{\beta}=(X^TX)^{-1} X^TY

对于只有两个解释变量的回归模型，可以得出参数最小二乘估计式的代数表达式：

β^2=∑yix2i∑x3i2−∑yix3i∑x2ix3i∑x2i2∑x3i2−(x2ix3i)2β^3=∑yix3i∑x2i2−∑yix2i∑x2ix3i∑x2i2∑x3i2−(x2ix3i)2β^1=Yˉ−β^2Xˉ2−β^3Xˉ3\begin{align} &\hat{\beta}_2=\cfrac{\sum y_ix_{2i}\sum x^2_{3i}-\sum y_ix_{3i}\sum x_{2i}x_{3i}}{\sum x_{2i}^2\sum x_{3i}^2-(x_{2i}x_{3i})^2} \\ &\hat{\beta}_3=\cfrac{\sum y_ix_{3i}\sum x^2_{2i}-\sum y_ix_{2i}\sum x_{2i}x_{3i}}{\sum x_{2i}^2\sum x_{3i}^2-(x_{2i}x_{3i})^2} \\ &\hat{\beta}_1=\bar{Y}-\hat{\beta}_2\bar{X}_2-\hat{\beta}_3\bar{X}_3 \end{align}

在软件中可以计算出来各个β\beta

和一元回归一样，我们可以定义：

拟合值
Y^i=β^0+β^1⋅Xi1+⋯+β^k⋅Xik\hat{Y}_i=\hat{\beta}_0+\hat{\beta}_1 \cdot X_{i1}+\cdots+\hat{\beta}_k \cdot X_{ik}

残差
u^i=Yi−Y^i\hat{u}_i=Y_i-\hat{Y}_i
残差，又称为剩余项

函数 名称 确定性 公式
总体回归函数 随机扰动项、误差项 确定 ui=Yi−E(Y∣Xi)u_i=Y_i-E(Y\mid X_i)
样本回归函数 残差、剩余项 不确定（看抽样情况） Yi−Y^i=eiY_i-\hat{Y}_i=e_i

参数最小二乘估计的性质

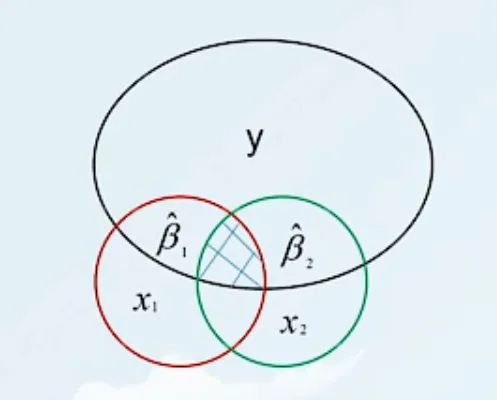
如何理解多元回归方程的系数？

Y^=β0^+β1^X1+β2^X2\hat{Y}=\hat{\beta_0}+\hat{\beta_1} X_1+\hat{\beta_2} X_2

  • β1^\hat{\beta_1} 是 X1X_1 对 Y 的纯影响
  • β2^\hat{\beta_2} 是 X2X_2 对 Y 的纯影响

多元回归有 k+1k+1 个条件

根据线性代数，由矩阵可以得出

β^2=∑i=1nr^i1yi∑i=1nr^i12\hat{\beta}_2=\cfrac{\sum\limits_{i=1}^n\hat{r}_{i1}y_{i}}{\sum\limits_{i=1}^n\hat{r}_{i1}^2}

Gauss-Markov定理

在六个基本假设成立的前提下，OLS估计量是 线性 无偏 最优估计量。

  • 线性

    • 可以表示成被解释变量y的线性函数 β^j=∑i=1nr^ij∑i=1nr^ij2yi\hat{\beta}_j=\sum\limits_{i=1}^{n}\cfrac{\hat{r}_{ij}}{\sum\limits_{i=1}^{n}\hat{r}_{ij}^2}y_{i}

  • 最优 在所有线性无偏估计量中，OLS估计量方差最小

  • 线性

  • 无偏性

    • E(β^)=βE(\hat{\beta})=\beta

  • 最小方差性

无偏性

  • 系数线性的回归方程
  • {(xi1,xi2,⋯ ,xik,yi):i=1,2,⋯n}\left\{(x_{i1}, x_{i2}, \cdots, x_{ik}, y_i):i=1,2,\cdots n\right\} 是随机样本
  • 解释变量无多重共线（线性无关）
  • E(u∣x1,x2,⋯ ,xk)=0E(u\mid x_1, x_2, \cdots, x_k)=0，任何一个 xix_i 都不和 uu 相关

定理
在假设一到四都满足的情况下，OLS估计量是无偏估计量，即

E(β^j∣x1,x2,⋯ ,xk)=βj,j=0,1,⋯ ,kE(\hat{\beta}_j\mid x_1, x_2, \cdots, x_k)=\beta_j, j=0, 1, \cdots, k

当抽样趋于无穷，估计值的均值越接近真实值

最小方差性

假设五（同方差性）：

var(u∣x1,⋯ ,xk)=σ2var(u\mid x_1, \cdots, x_k)=\sigma^2

u在xix_i 的条件方差等于 σ2\sigma^2

如果假设一到五都成立，那么
var(β^j∣x1,⋯ ,xk)=σ2SSTj(1−R2),j=1,2,⋯ ,kvar(\hat{\beta}_j\mid x_1, \cdots, x_k)=\cfrac{\sigma^2}{SST_j(1-R^2)}, j=1,2,\cdots, k
SSTj=∑j=1n(xij−xˉj)2,j=1,2,⋯ ,kSST_j=\sum\limits_{j=1}^{n}(x_{ij}-\bar{x}_j)^2, j=1,2,\cdots, k

其中，Rj2R^2_j 是拿其他解释变量做回归得到的拟合优度

注意：
关于 var(β^0∣x1,⋯ ,xk)var(\hat{\beta}_0\mid x_1, \cdots, x_k) ，并没有给出相应公式，因为无法得到 1−R021-R_0^2 的数值。为了在多元回归里计算 var(β^0∣x1,⋯ ,xk)var(\hat{\beta}_0\mid x_1, \cdots, x_k) 需要使用矩阵相关知识

σ^2=∑i=1nu^i2n−k−1\hat{\sigma}^2=\cfrac{\sum\limits_{i=1}^{n}\hat{u}_i^2}{n-k-1}

在假设一到五成立的基础上，E(σ^2∣x1,x2,⋯ ,xk)=σ2E(\hat{\sigma}^2\mid x_1, x_2, \cdots, x_k)=\sigma^2

最小二乘估计的分布性质

E(βj^)=βVar(βj^)=σ2cjjβj^∼N[βj,σ2cjj]\begin{aligned} E(\hat{\beta_j})&=\beta \\ Var(\hat{\beta_j})&=\sigma^2c_{jj} \\ \hat{\beta_j}&\sim N\left[ \beta_j, \sigma^2c_{jj}\right] \end{aligned}

其中，cjjc_{jj} 是矩阵 XTXX^TX 中的元素

随机扰动项方差的估计

基本方法和一元线性回归一致。

无偏估计

σ^2=1n−k∑ei2\hat{\sigma}^2=\cfrac{1}{n-k}\sum e^2_i

则方差

Var^(β^2)=σ^2cjj=(1n−k∑ei2)cjj\widehat{Var}(\hat{\beta}_2)=\hat{\sigma}^2c_{jj}=\left(\cfrac{1}{n-k}\sum e^2_i\right)c_{jj}

多元的假设检验和区间估计

假设检验

为说明多元线性回归线对样本观测值的拟合情况，我们可以通过拟合优度的判断，利用多重可决系数，考察被解释变量的总变差中由多个解释变量来做出解释的那部分变差的比重。在此基础上，还需要通过回归系数的显著性检验，得到回归系数的可靠估计量。

拟合优度

一元线性回归中我们使用了可决系数R2R^2，来衡量估计的模型对观测值的拟合程度。在多元回归中，同样可以使用这样的方法。

由于是多元线性回归，存在多个解释变量。对被解释变量YY的变差分解如下：

变差∑(Yi−Yˉ)2=∑(Yi−Yˉ)2+∑(Yi−Yˉ)2TSS=ESS+RSS自由度(n−1)=(k−1)+(n−k)\begin{aligned} 变差& &\sum(Y_i-\bar{Y})^2 &=\sum(Y_i-\bar{Y})^2+\sum(Y_i-\bar{Y})^2 \\ & & TSS &=ESS + RSS \\ 自由度& & (n-1)&=(k-1)+(n-k) \end{aligned}

和一元类似，

R2=ESSTSS=1−RSSTSSR^2=\cfrac{ESS}{TSS}=1-\cfrac{RSS}{TSS}

如果考虑自由度，对可决系数进行修正，可以得到：

Rˉ2=1−RSS/(n−k)TSS/(n−1)\bar{R}^2=1-\cfrac{RSS/(n-k)}{TSS/(n-1)}

显著性检验

在一元回归在我们使用过t检验，在此处同理可以使用t检验，检查回归参数的显著性。除此之外，我们还可以使用F检验，检查回归方程的显著性。

F检验

研究被解释变量和所有解释变量之间的线性关系是否显著，我们通常使用 F检验

F分布相关知识
X∼χ2(n1),Y∼χ2(n2)X\sim \chi^2(n_1),Y\sim \chi^2(n_2)

X/n1Y/n2∼F(n1,n2)\cfrac{X/n_1}{Y/n_2}\sim F(n_1, n_2)

1F(n1,n2)=F(n2,n1)\cfrac{1}{F(n_1, n_2)}=F(n_2,n_1)

我们假设：

H0:β2=β2=⋯=β2=0H1:βj(j=2,3,⋯不全为零)这应该是一个单侧检验\begin{aligned} &H_0: \beta_2=\beta_2=\cdots=\beta_2=0 \\ &H_1: \beta_j (j=2,3,\cdots不全为零)_{这应该是一个单侧检验} \end{aligned}

在 H0H_0 成立的基础上，构造统计量

F=ESS/(k−1)RSS/(n−k)∼F(k−1,n−k)F=\cfrac{ESS/(k-1)}{RSS/(n-k)}\sim F(k-1,n-k)

计算观测值，如果F>Fα(k−1,n−k)F> F_{\alpha}(k-1,n-k)，那么就拒绝原假设，说明回归方程显著，计入模型的解释变量对被解释变量有显著影响。反之没有显著影响。

一元线性回归中，解释变量只有一个，不存在整体检验的问题。此时进行F检验，和t检验是一样的。

F=ESS/(2−1)RSS/(n−k)=t2F=\cfrac{ESS/(2-1)}{RSS/(n-k)}=t^2

同时可以发现，F统计量和可决系数R2R^2有很大关系，区别在于前者考虑了自由度，后者没考虑自由度，可决系数指出了拟合程度，而F检验能告诉我们确定的界限

F=n−kk−1⋅R21−R2F=\cfrac{n-k}{k-1}\cdot\cfrac{R^2}{1-R^2}

t检验

再多元回归中，我们同样可以对回归参数（系数）进行估计，对解释变量进行显著性检验。由于存在多个解释变量，因此我们对每个解释百年来进行显著性检验，可以得出当其他解释变量不变时，该解释变量是否对被解释变量有显著影响。

我们已经知道参数的性质：

βj^∼N[βj,σ2cjj]\hat{\beta_j}\sim N\left[ \beta_j, \sigma^2c_{jj}\right]

因此，参数符合正态分布，构造Z统计量

Z=β^j−βjVar(β^j)∼N(0,1)Z=\cfrac{\hat{\beta}_j-\beta_j}{\sqrt{Var(\hat{\beta}_j)}}\sim N(0, 1)

我们已知 Var(βj^)=σ2cjjVar(\hat{\beta_j})=\sigma^2c_{jj} ，但是由于不知道σ2\sigma^2，我们使用其无偏估计 σ^2=1n−k∑ei2\hat{\sigma}^2=\cfrac{1}{n-k}\sum e^2_i ，得到：

Var^(β^2)=σ^2cjj=(1n−k∑ei2)cjj\widehat{Var}(\hat{\beta}_2)=\hat{\sigma}^2c_{jj}=\left(\cfrac{1}{n-k}\sum e^2_i\right)c_{jj}

构造t统计量

t=β^j−βjVar^(β^j)=β^j−βjσ^cjj=∼t(n−k)t=\cfrac{\hat{\beta}_j-\beta_j}{\sqrt{\widehat{Var}(\hat{\beta}_j)}}=\cfrac{\hat{\beta}_j-\beta_j}{\hat{\sigma}\sqrt{c_{jj}}}=\sim t(n-k)

假设检验：

H0:βj=0(j=1,2,⋯ ,k)H0:βj≠0(j=1,2,⋯ ,k)\begin{aligned} &H_0: \beta_j=0 &(j=1, 2, \cdots, k)\\ &H_0: \beta_j\neq0 &(j=1, 2, \cdots, k) \end{aligned}

置信区间−tα/2(n−k)≤t≤tα/2(n−k)-t_{\alpha/2}(n-k)\le t\le t_{\alpha/2}(n-k)

如果∣t∗∣≤tα/2\vert{t^*}\vert \le t_{\alpha/2}，说明影响显著。

区间估计

和一元基本一致，根据无偏估计写出构造的统计量，划分临界值得出置信区间。

预测

点预测

把各个解释变量的值带入估计的样本回归函数得出的就是点预测值。

平均值区间预测

实质是分析点预测值和平均值的关系，分析概率密度分布性质。记他们的偏差为

wf=Y^f−E(Yf)w_f=\hat{Y}_f-E(Y_f)

E(wf)=0E(w_f)=0

可以知道偏差同样符合正态分布，有

wf∼N[0,σ2Xf(XTX)−1XfT]w_f\sim N\left[0, \sigma^2X_f(X^TX)^{-1}X^T_f\right]

用σ^2\hat{\sigma}^2构造统计量，得到

t=w^−E(wf)SE(wf^)=Y^f−E(Yf)σ^Xf(XTX)−1XfTt=\cfrac{\hat{w}-E(w_f)}{SE(\hat{w_f})}=\cfrac{\hat{Y}_f-E(Y_f)}{\hat{\sigma}\sqrt{X_f(X^TX)^{-1}X^T_f}}

个别值区间预测

个别值偏差

ef=Y^f−Y^fe_f=\hat{Y}_f-\hat{Y}_f

E(ef)=0E(e_f)=0

Var(ef)=σ2[1+Xf(XTX)−1XfT]Var(e_f)=\sigma^2[1+X_f(X^TX)^{-1}X^T_f]

接下来

  • 无偏估计
  • 构造统计量符合t∼t(n−k)t\sim t(n-k)
  • 根据置信水平，得出临界值，写出预测区间

Stata常用命令

与OLS有关的命令有两个：

regress

用OLS的方法来估计线性回归方程的系数

  • regress [被解释变量], [解释变量] (if条件语句)

例如：regress wage education experience，wage是 被解释变量，education 和experience 是两个 解释变量

例如：regress wage education experience if female==1加上性别为女的条件

predict

用来得到拟合值或残差，必须在回归命令regress之后使用

  • predict [新变量] 用于得到拟合值
  • predict [新变量], residuals 用于得到残差
    例如：
1
2
regress wage education exprience
predict wage_hat

先对变量进行回归，然后拟合 wage^\hat{wage}

1
2
regress wage education exprience
predict resi, residuals

在新的变量里得到残差的估计值

Model对应的就是SSE，Residual对应SSR，Total对应SST

第一行wage是被解释变量，下面是解释变量。Coef. 是估计值，Std. Err 是估计量的标准差