每个孩子都是一株小草，各不相同，生长顺序也不一样，耐心的守在小草们的旁边，见证他们多样的成长。我们终究是过客，好好守护这份师生缘。 过完繁重的考试周，转头又踏上了前往贵州的征途。数千公里的跨越，每离贵州

去远方吧，去一个充满浪漫和希望的地方。 连续多日连轴转，几乎难以坐下静心休息片刻。整个假期确实变得无比充实，同时更意味着变得更加需要担当。常青藤支教队的各位同志来自五湖四海，跨越山海奔赴到共同的目的地，心怀一个共同的梦想：播下一颗种子，一颗属于希望的种子。在爱的滋润下，这颗种子会生根发芽，成为孩子们未来前行路上的一片荫庇，一座灯塔，一座。 每个孩子都是一株小草，各不相同，生长顺序也不一样，耐心的守在小草们的旁边，见证他们多样的成长。

本文不是严谨的投资分析，更不可当作投资建议，仅仅是我的课程论文，放在此处备份，以提供参考。投资有风险，投资需谨慎。务必注意分析的时效性。 关键词：持续破圈 多元化 影视 视频平台 基本面分析 宏观经济分析 政策因素 哔哩哔哩作为中国年轻一代的标志性品牌及领先的视频社区，受益于国家对文化创意产业的支持和鼓励。 哔哩哔哩在2020年3月28日在美国纳斯达克全球精选市场上市，代码为“BILI”，在2021年3月29日在香港联合交易所完成双重主要上市，代码为“9626”。这体现了哔哩哔哩在国际资本市场的认可和影响力。 哔哩哔哩在环境、社会及治理（ESG）方面做出了一系列努力，包括推动绿色低碳发展，支持公益慈善事业，保护用户隐私和数据安全，维护网络生态和版权秩序等。这有助于提升哔哩哔哩的社会责任感和品牌形象。 技术因素 哔哩哔哩拥有强大的技术实力和创新能力，不断推出新的产品和功能，满足用户的多元化需求。例如，哔哩哔哩推出了互动视频、直播电商、音频、动态漫画等多种形式的内容。 哔哩哔哩利用人工智能、大数据、云计算等先进技术，提升用户体验和运营效率。例如，哔哩哔哩使用人工智能技术进行内容审核、推 ...

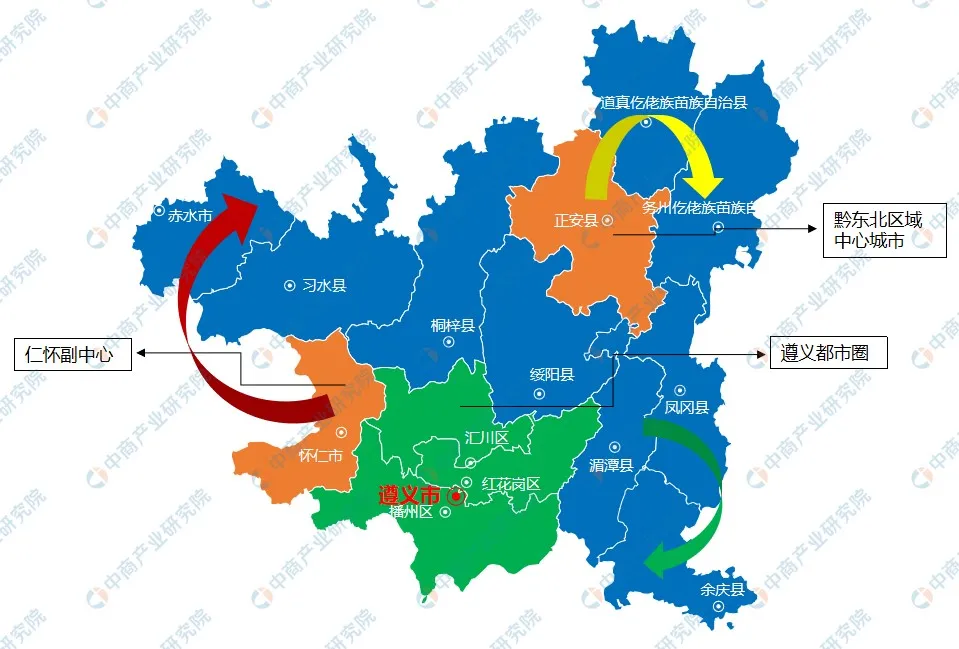
关于贵州省遵义市仁怀市的高粱种植对当地经济的促进的调查报告大纲如下： 仁怀市的高粱种植现状：仁怀市是贵州省重要的高粱种植区，主要生产酒用红高粱，是茅台酒的主要原料来源。仁怀市高粱种植面积达30万亩，年产量近10万吨，年产值近10亿元¹²。仁怀市高粱种植涉及14个乡镇，29万余户农户，亩均收入2000元以上²。 仁怀市的高粱种植特点：仁怀市高粱种植依托赤水河流域的特有土壤和气候条件，选育出优良品种，实行高标准生产，推广有机、绿色、标准化、规模化、订单式种植模式，建立了完善的质量检测和追溯体系，形成了“红缨子”“红珍珠”等品牌²³。仁怀糯高粱是全国农产品地理标志，其籽粒饱满、粒小皮厚、角质率高、耐蒸煮，适合酿造茅台酒⁴。 仁怀市的高粱产业发展对策：仁怀市将高粱产业作为乡村振兴的重要抓手，坚持以茅台集团为龙头，以其他地方白酒企业为补充，构建产业链和供应链，提升高粱收储和加工能力，拓展高粱深加工和综合利用领域，打造高粱文化和旅游品牌，促进农民增收和乡村发展¹²。 源: 与必应的对话， 2023/7/8 (1) 在希望的田野上 | 贵州仁怀30万亩高粱大丰收 高标准生产促农 … https: ...

证券概念及类型 证券概念 广义证券 证券是多种经济权益凭证的统称，是指用来证明持券人有权按其券面所载内容取得应有权益的书面证明。 广义上，主要包括资本证券、货币证券、财务证券、凭证证券 狭义证券 特指资本证券 证券类型 根据证券持有人收益性不同 无价证券：是指不能使持券人或第三者取得一定收入的证券，如收据、借据、保险单、供应证和购物券等。 有价证券：是指具有一定的票面金额，证明持券人对某种资产拥有所有权或债权，有权按期取得一定收入的书面凭证。 根据构成内容不同 商品证券：是对一定量的商品拥有索取权的凭证； 如：提货单、栈单、购物券 货币证券：是对一定量的货币拥有索取权的凭证； 如：支票、期票、本票、汇票 商业证券：商业汇票和商业本票 银行证券：银行汇票、银行本票和支票 资本证券：是有价证券的主要形式，它是对一定量的资本拥有所有权和对一定的收益分配拥有索取权的凭证； 如：股票、债券 根据发行者的性质分 直接证券：非金融机构发行的证券 间接证券：金融机构发行的证券 根据市场的流通性分 适销证券：可以经过转让而自由流通的证券 非适销证券 ...

在这一章中，我们考虑 变量 出现特殊情况时的研究。 滞后变量 在过往章节中，我们都认为变量是随机的。但考虑现实情况，以下两种变量存在特殊情况： 滞后变量 某一期的数据会对今后多期数据产生“深远影响”。 如果只是解释变量存在滞后，我们就称之为 分布滞后模型； 如果只是被解释变量存在滞后，我们就称之为 自回归模型 分布滞后 根据滞后的不同特点（过去经验对未来数据的影响程度），我们一般分为： 递减滞后 不变滞后 倒 ∧\land∧ 形 核心假设 一件事情能带来的影响是基于事情本身的，滞后变量的取值来源于原始数据，再根据经验乘上对应结构的权数，有 滞后数据=原始数据×权数滞后数据=原始数据\times 权数 滞后数据=原始数据×权数 把多个滞后变量合成一个新的变量 ZtZ_tZt​，回归方程就是 Yt=α0+β0Zt+μtY_t=\alpha_0+\beta_0 Z_t +\mu_t Yt​=α0​+β0​Zt​+μt​ 这个方法就是 经验加权估计法 为了增加说服力，我们可以选不同的滞后结构多加权几次，选R2R^2R2、FFF 值、ttt 值 、DWDWDW 值最佳的那一种 ...

特殊？ 数据的特殊：时间序列数据 平稳性假设，通过单位根检验是否平稳，非平稳又是单整，去看是否协整（EG两步法，），得到误差修正模型。不协整就是伪回归无法估计。 方程的特殊：多方程联立 经典计量经济学在多个方面有假设： 随机扰动项满足极限法则和由极限法则导出的基本假设 时间序列性的平稳性 时间序列性的平稳性及其检验 平稳性假设 严格平稳：与时间位移无关 弱平稳：YtY_tYt​ 的期望、方差、协方差不随时间改变 但是现实中数据不一定平稳，例如GDP的变动，非平稳数据可能导致 伪回归问题。 这是由于Yt=γYt−1+ϵtY_t=\gamma Y_{t-1}+\epsilon tYt​=γYt−1​+ϵt这样的白噪声 如果γ=1\gamma=1γ=1，说明前后变化是纯粹随机的（随机游走过程），白噪声的累计导致误差越来越大。 检验（DF检验） 原假设：γ=1\gamma=1γ=1 协整与误差修正模型 非平稳的变量的线性组合平稳，叫做 协整 意味着本应该无限大的随机误差得到了修正。 我们可以作协整检验（EG两步法） 方程组偏倚性及其检验 互为因果导致解释变量和随机扰 ...

引言 在前几章的内容中提出符合古典假设的线性回归模型，所谓古典假设是指: 简单线性回归基本假定 假定一 零均值假定，即随机扰动项的条件期望等于0 假定二 同方差假定，即对于每一个给定的 XiX_iXi​，随机扰动项的条件方差都等于 σ2\sigma^2σ2 Var(ui∣Xi)=E[ui−E(ui∣Xi)]2=E(ui2)=σ2Var(u_i\mid X_i)=E[u_i-E(u_i\mid X_i)]^2=E(u_i^2)=\sigma^2 Var(ui​∣Xi​)=E[ui​−E(ui​∣Xi​)]2=E(ui2​)=σ2 假定三 无自相关假定，即各个扰动项的逐次值互不相关，也可以说他们的协方差等于零 Cov(ui,uk)=E[ui−E(ui)]E[uk−E(uk)]={σ2,i=k0,i≠k(i,k=1,2,3,⋯n)\begin{aligned} Cov(u_i, u_k)&=E[u_i-E(u_i)]E[u_k-E(u_k)]\\ &=\begin{cases} \sigma^2, &i=k \\ 0, & ...

“金融服务对贫困人群来说就像氧气一样重要，如果没有金融服务，就会造成贫困以及其他各种问题，甚至导致生存问题。” 本学期我阅读的第一本书，是尤努斯的《穷人的银行家》尤努斯用27美元探索出的普惠金融之路，帮助了全世界无数受限于金融机构的穷人得以发现拜托贫困的上升之道，正如尤努斯的理想：看到这个世界摆脱贫困。“这意味着，在这个星球上没有一个人会被描述为穷人，没有一个人的基本需求不能得到满足。到那时，“贫困’这个词将不再具有实用的意义，它将只被用来理解过去。贫穷的位置，只应在博物馆里。” 默罕默德·尤努斯是一位孟加拉国的银行家、经济学家和教授，也是2006年诺贝尔和平奖的得主。他以创立孟加拉乡村银行（又名格莱珉乡村银行）而闻名于世，这是一家专门为贫困人士提供小额贷款的银行，被认为是微型金融的先驱和创新者。 尤努斯的故事始于1976年，当时孟加拉国正遭受大饥荒的困扰，数以万计的人死于饥饿和疾病。尤努斯当时是吉大港大学的经济学教授，他感到自己所教授的经济理论与现实生活脱节，无法解决人民的痛苦。他决定走出校园，到附近的村庄去了解穷人的生活状况和需求。 在村庄里，他发现了一个令他震惊的事实：许多贫 ...

本学期我阅读的第三本书是阚治东的《荣辱二十年》。二十年的光阴蹉跎，中国第一代证券先锋阚治东的人生起起落落，看过山巅的风景，也感受过谷底的滋味。阚治东的人生之路，也是中国证券市场发展的一个缩影与见证。 泰戈尔曾言：人的记忆力是有限的，不是所有经历过的人和事都能永存我们的记忆之中。有如泰戈尔诗中所表述的，“鸟儿已飞过，天空没有翅膀的痕迹。”但有些人和事，即使你不用心去记，它们也仿佛镶嵌在你的脑海里，留下永久的印痕，并且，随着时间的推移，这种印痕会越来越清晰。几次风波对阚治东而言或许也是这样的感受。1999年，应深圳市政府的邀请，阚治东执掌深圳创新科技投资公司，深创投后被评为国内最好的创业投资机构；2002年，阚治东重返证券业，作为“救火队长”空降千疮百孔的南方证券，出任总裁，最终未能力挽狂澜，反而被关押了21 天。当他被迫进入看守所，脱下昂贵的手表和体面的西服，转而变为一名普通的看守所犯人，难以想象这样的落差感对人的冲击是何等强烈。 阚治东自己坦言牢狱之灾的缘由：第一次在上海，沪深两市争夺金融中心的激斗，阚治东为上海市政府领导的默许定了雷背了黑锅；第二次在深圳去南方证券救火无力回天，最后公 ...

本学期我阅读的第二部书，是罗伯特希勒的《金融与好的社会》。有人如是说：总的来说，这本书似乎是对于某一终极问题或命题——“这个世界会好吗”——的另一种回答或者是“金融版”回答。梁漱溟先生的《这个世界会好吗》、爱因斯坦的《人类的未来会好吗》都尝试回答了这个问题，一个是文化的角度、一个是科学的视角，本书则是以金融为出发点和方法论。 幼年时代起，我便对世界的运行产生了极大的好奇：好的社会究竟是什么样子？现代社会的几大支柱是如何构建的？翻开书页，一段话引入眼帘：“金融是一门关于目标构筑的学科，是一种研究如何激励更多人为了共同的目标而努力奋斗的学问，同时也注重研究如何使时间的推移和人员的变化不对追逐目标的努力造成负面影响。” 西方的亚当斯密对社会的运行提出自己的解决之道：引入看不见的手，遵从市场规律并利用之，企图以此激发社会的劳动参与和生产进步。历史的长河告诉我们，经济的运行并非单纯仅靠市场变动或政府管控就得以通畅运行，而社会的运行也并非仅靠金融的博弈就得以高枕无忧。回望中国发展之路，我们不禁对诸多历史产生好奇：改革开放的宏伟蓝图是如何带领经济昂扬鹏飞？转移支付的大幅实施体现了金融与社会的何种关系 ...

统计出单链表HL中结点的值等于给定值X的结点数。 int CountX(LNode* HL,ElemType x) 1234567891011121314151617int CountX(LNode* HL,ElemType x){ //定义一个计数器，初始为0 int count = 0; //定义一个指针，指向单链表的第一个结点 LNode* p = HL->next; //遍历单链表，直到遇到空指针为止 while(p != NULL){ //如果当前结点的值等于给定值x，那么计数器加一 if(p->data == x){ count++; } //指针后移，指向下一个结点 p = p->next; } //返回计数器的值 return count;} 设有一组初始记录关键字序列（K1，K2，…，Kn），要求设计一个c语言算法能够在O(n)的时间复杂度内将线性表划分成两部分，其中左半部分的每个关键字均小于Ki，右半部分的每个关键字均大于等于Ki。 ...

基础知识 光圈 焦距 P档 P档的最明显特点就是程序自动曝光，与此相关的还有AE自动曝光 图像亮度（曝光补偿） 为了更改图片亮度，在这部分可以做 设置曝光补偿 锁定曝光或对焦 测光 更改测光方式 测光和对焦一起自动调整 感光度 感光度变率 高感光度下调整降噪级别 曝光模式 自动包围曝光 亮度校正 对比度矫正 过度曝光修复（高光细节） 暗部修复（暗部细节） 中性灰滤镜（更慢快门速度、更小光圈，降低光强度） 使点测光AE区框与自动对焦框一起移动的方法： ISO感光度 ISO的适用范围 更改降噪级别 高ISO可能导致高噪点，因此可以更改降噪级别降低噪点。 注意，此功能只可以在JPEG画质下开启。 自动包围曝光 此功能可以调整曝光不足或者曝光过度时的曝光度 颜色和连续拍摄 白平衡 自动 自定义 手动矫正 色调 不同模式色调 自定义色彩 拍摄模式 单张 连续 自拍 延时 拍摄范围与对焦

前言 微软输入法是系统的自带输入法，实际上在现在的系统版本下，微软输入法功能已经可以十分强大。经过些许摸索，在此处记录对输入法的调教记录，后续会根据需要继续修改。 在输入法设定区域右键单击就可以看到微软输入法的相关设置，在此处可以对外观设置、按键设置、词库设置等进行修改。 外观 可以为输入法选择炫酷的界面 如图所示，此处可以设置： 更多的候选词数，方便选词 候选项字体大小（防止老花眼） 文本输入主题（炫酷皮肤） 输入法工具栏是否开启（我自己不太喜欢一直挂着所以没开） 词库 专业词典 自定义词库 引用站外地址 化学输入法补丁 パチュリーPatchouli 本次调教也是缘于看到这个视频，用自定义词库的方式提高化学用语的输入效率，方便在没有Latex的环境下快捷输入化学式等。 按键配置 开启逗号句号切换~

停更原因（事故救命） 很长一段时间没有更新，原因是我的移动硬盘挂了。由于当初买电脑预算有限，选择了500gb的版本肯定是不够的，因此我用硬盘盒+机械硬盘的方法DIY了移动硬盘。这样的组合虽然有性价比的优势，但是机械盘注定命途多舛，不能磕碰。果不其然，在三月初某一天我用兄弟的台式机渲染视频时，兄弟不小心磕碰到硬盘，随后就无法写入数据。打开硬件管理器发现磁盘占用是100%，但是速度为零，耳朵凑近一听就听到了呲呲声，初步判断应该是磁头出问题肯定得开盘了，随后就马上断电准备开盘恢复数据（大悲剧）。 这次硬盘故障导致面临几个大问题： 硬盘存了以前所有照片视频非常珍贵 硬盘存了平时学习资料，各种作业全在里面 硬盘也是存储我博客数据的地方，故障之后就没法更新博客 在淘宝上找到数据恢复的地方之后马上前往恢复数据。这家店铺老板很良心，将近2T的数据也只收了450（想到上次开盘1T就收五百块）。随后恰好看到固态价格大跳水，入手了爱国者P7000Z。这块硬盘好处是： 价格便宜。加上京东各种券最后510就拿下。 长江颗粒，性能也很棒。参数来看这块硬盘是一颗PCIE4.0满速盘，读写7000多（坑比G15 ...

引言 随全球经济增长放缓、疫情后产能释放以及竞争加剧等因素，2022年韩国贸易收支出现472亿美元的逆差，创历史新高1。贸易形式恶化和受其影响的工业领域方面的萎靡、银行业的萎缩引起了广泛关注。被视为“全球贸易晴雨表”的韩国2，由于其特殊的国际贸易地位，其经济形势的波动对全球经济有着重要的指示作用和导向作用。当前韩国面临着产业升级的挑战和机遇，以期摆脱逆差困境。而中国当前正致力于解决人民日益增长的美好生活需要和不平衡不充分的发展之间的矛盾，迫切需要深化产业升级，以推动生产力发展，实现共同富裕。文章通过对比分析韩国和中国的发展经验，不仅对中国产业升级有积极的借鉴作用，也对如何在未来应对贸易逆差、贫富分化、人口老龄化等问题提供了有益的启示。 本文通过分析韩国不同时期的国际贸易商品结构变化，以说明其对外贸易政策的演变情况，进而运用比较优势、产业生命周期等经济学国际贸易理论，探索两者之间的关系，从而为今后优化我国贸易结构提供参考依据。 韩国贸易结构和国际贸易政策概述 贸易结构的动态演变 贸易结构是一国经济结构的重要方面。贸易结构优化可能对于一国贸易发展和国内产业结构升级有积极作用，有助于推动贸易 ...

一个简单的逻辑是： 当时东南亚各国多年来经济高速发展，以出口替代为导向的经济政策和金融自由化的风潮吸引了外资大量流入，存在大量的逆差，造成了“错配”的情况：一是货币错配，二是期限错配。由此导致这些国家的资本结构、外债结构存在巨大风险：大量流入的外资存款在国内被用于房地产、制造业等中长期贷款中，一旦外资流出超过流入，本币的贬值就不可避免。以索罗斯为代表的西方资本家此时观察到这一情况，一方面做空股市，一方面大量卖出本币，买进外币，导致货币被做空、货币贬值，汇率暴跌。 做空 做空是指投资者借入某种货币，然后卖出换成另一种货币，期待借入的货币贬值，从而在还款时获利。做空会导致贬值的原因是，做空会增加市场上借入货币的供应量，而供需理论告诉我们，供应量增加会导致价格下降。当市场上有大量的投机者或对冲基金做空某种货币时，就会形成一种自我实现的预期，导致该货币的需求减少，进一步推动其贬值。 做空会导致贬值的原因是，做空会增加市场上借入货币的供应量，而供需理论告诉我们，供应量增加会导致价格下降。当市场上有大量的投机者或对冲基金做空某种货币时，就会形成一种自我实现的预期，导致该货币的需求减少，进一步 ...