概率论与数理统计 | 课程学习纲要
概率论与数理统计 | 课程学习纲要
Prong本文使用new Bing书写
知识体系
这门课程的知识体系可以分为两大部分,即概率论和数理统计。
概率论
研究随机现象的规律性的数学分支,主要包括以下几个方面的内容2:
概率论的基本概念
如事件、概率、条件概率、独立性等,以及一些常用的概率计算公式,如加法公式、乘法公式、全概率公式、贝叶斯公式等。这部分内容是概率论的基础,是理解和运用概率论的前提。
随机变量及其概率分布
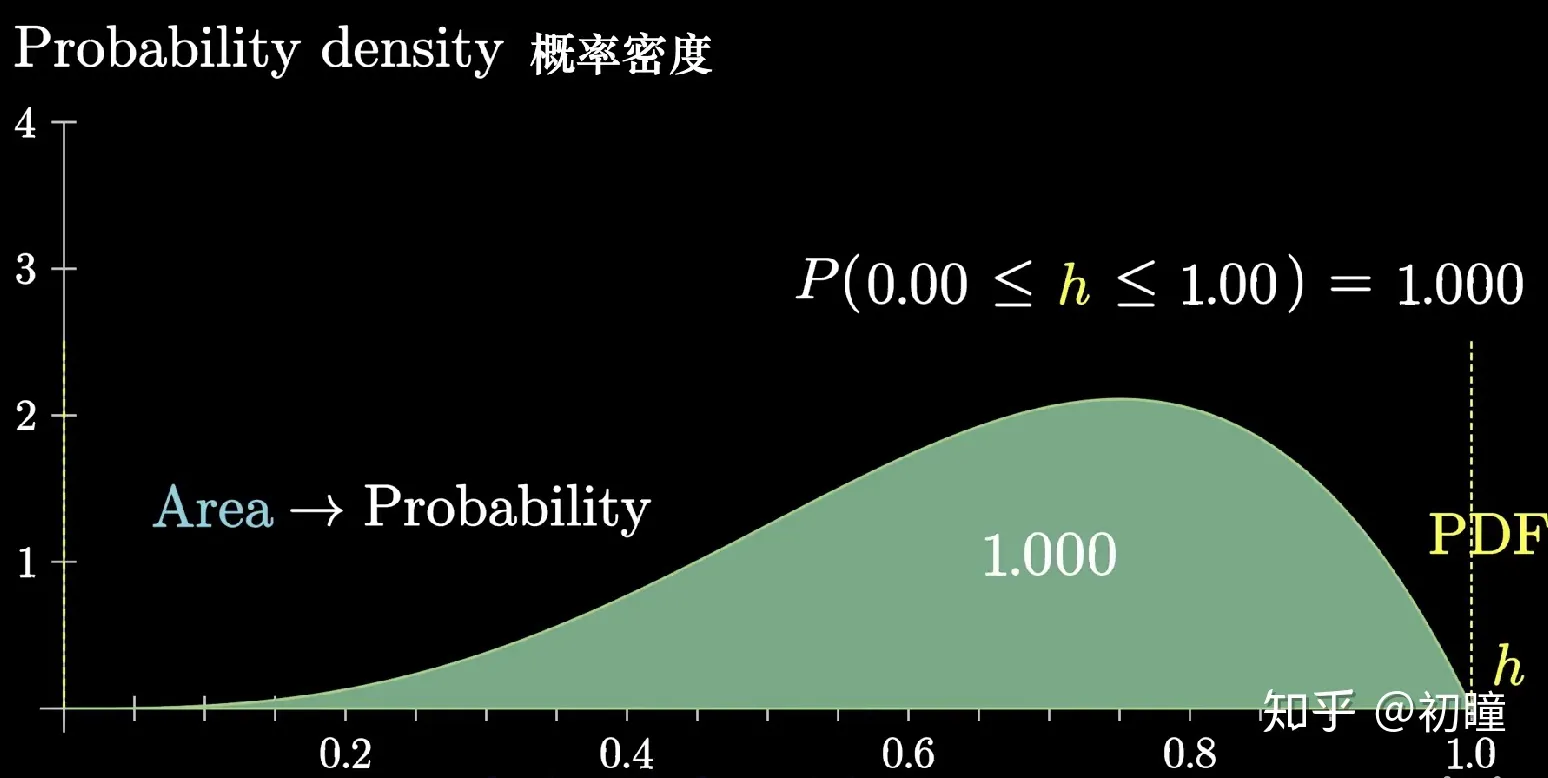
包括离散型随机变量和连续型随机变量的定义、分布函数、概率密度函数等概念,以及一些常见的概率分布,如二项分布、泊松分布、正态分布、指数分布、均匀分布等,以及它们的性质和应用场景。这部分内容是概率论的核心,是描述和分析随机现象的主要工具。
数字特征
包括随机变量的数学期望、方差、协方差、相关系数等数字特征,以及它们的性质和意义,以及如何利用它们描述随机变量的分布特征和相关性。这部分内容是概率论的重要内容,是对随机变量进行定量分析的基本方法。
大数定律与中心极限定理
如切比雪夫大数定律、伯努利大数定律和辛钦大数定律等大数定律的内容和意义,以及棣莫弗-拉普拉斯定理和列维-林德伯格定理等中心极限定理的内容和意义,以及如何利用它们进行近似计算和推断。这部分内容是概率论的高级内容,是揭示随机现象的规律性和普遍性的重要定理。
数理统计
研究如何利用统计方法对随机现象进行推断和决策的数学分支,主要包括以下几个方面的内容2:
统计量及其概率分布
如统计量的定义、性质和分类,以及一些常用的统计量,如样本均值、样本方差、样本相关系数等,以及它们的概率分布,如卡方分布、t分布、F分布等,以及它们的性质和应用场景。这部分内容是数理统计的基础,是建立统计推断的前提。
参数估计
如参数估计的基本思想和方法,如矩估计法和最大似然估计法,以及如何构造点估计和区间估计,以及估计量的优良性判别准则。这部分内容是数理统计的核心,是运用统计方法进行推断和决策的主要方法之一。
假设检验
如假设检验的基本思想和方法,如参数检验和非参数检验,以及如何构造检验统计量和判断检验结果,以及检验的显著性水平和功效等概念。这部分内容是数理统计
学习顺序
首先,学习概率论的基本概念,掌握事件、概率、条件概率、独立性等基本概念,以及一些常用的概率计算公式,如加法公式、乘法公式、全概率公式、贝叶斯公式等。这部分内容是概率论的基础,是理解和运用概率论的前提。
其次,学习随机变量及其概率分布,掌握离散型随机变量和连续型随机变量的定义、分布函数、概率密度函数等概念,以及一些常见的概率分布,如二项分布、泊松分布、正态分布、指数分布、均匀分布等,以及它们的性质和应用场景。这部分内容是概率论的核心,是描述和分析随机现象的主要工具。
然后,学习数字特征,掌握随机变量的数学期望、方差、协方差、相关系数等数字特征,以及它们的性质和意义,以及如何利用它们描述随机变量的分布特征和相关性。这部分内容是概率论的重要内容,是对随机变量进行定量分析的基本方法。
接着,学习大数定律与中心极限定理,掌握切比雪夫大数定律、伯努利大数定律和辛钦大数定律等大数定律的内容和意义,以及棣莫弗-拉普拉斯定理和列维-林德伯格定理等中心极限定理的内容和意义,以及如何利用它们进行近似计算和推断。这部分内容是概率论的高级内容,是揭示随机现象的规律性和普遍性的重要定理。
紧接着,学习统计量及其概率分布,掌握统计量的定义、性质和分类,以及一些常用的统计量,如样本均值、样本方差、样本相关系数等,以及它们的概率分布,如卡方分布、t分布、F分布等,以及它们的性质和应用场景。这部分内容是数理统计的基础,是建立统计推断的前提。
最后,学习参数估计和假设检验,掌握参数估计的基本思想和方法,如矩估计法和最大似然估计法,以及如何构造点估计和区间估计,以及估计量的优良性判别准则。掌握假设检验的基本思想和方法,如参数检验和非参数检验,以及如何构造检验统计量和判断检验结果,以及检验的显著性水平和功效等概念。这部分内容是数理统计的核心,是运用统计方法进行推断和决策的主要方法。