概率论与数理统计 | 常见的分布

排序
k个东西排序，第k个有k种可能位置，第k-1个有k-1种，以此类推，排序可能性为

$$k!=k \times (k-1) \times (k-2) \times \dots \times 1$$

组合(选取)
n个中选出r个对象，不考虑顺序，求出对象选取有多少种可能情况

$$C_n^k=\cfrac{n!}{k!(n-k)!}=\cfrac{A_n^k}{k!}$$

排列(选取再排序)

$$A_n^k=\cfrac{n!}{(n-k)!}=C_n^k \times k!$$

• 第一步，从n中选出k个，不考虑次序
• 第二步，对每个组合再进行排序，$\times k!$

离散型

0~1分布

$X \sim B(x, p)$,

有两种结果，试验只做一次

二项分布的特殊情况

数学期望为$E(X)=p$，方差为$D(X)=p(1-p)$

几何分布

$X \sim G(p)$, $Geometric$

$$P\{X=K \}= (1-p)^{K-1}p$$

第k次首次发生，此前k-1次均未发生

二项分布

$X \sim B(n, p)$, $Binomial$

$$P\{X=K\}=C_{n}^{k}p^k(1-p)^{n-k}, \text {k=0, 1, 2, 3...n}$$

n次试验发生了k次

数学期望为$E(X)=np$，方差为$D(X)=np(1-p)$

最可能值

• $(n+1)p$不为整数，$[(n+1)p]$取整达到最大值
• $(n+1)p$不为整数，$(n+1)p$, $(n+1)p-1$达到最大值

具有可加性

近似求值

二项分布用泊松分布来近似
n比较大，p比较小，np适中
$n\ge 100$, $np \le 10$
$np=\lambda$

二项分布用正态分布来近似 (de Moivre - Laplace)棣莫佛－拉普拉斯定理
n比较大，np也比较大

$$\lim_{x \to \infty} P(\cfrac{Y_n-np}{\sqrt{np(1-p)}}\le x)=\Phi_0(x)$$

• $P(X \le k)$
  $Y=\cfrac{X-np}{\sqrt{np(1-p)}}, P(X \le k)=P(Y \le \cfrac{k-np}{\sqrt{np(1-p)}})=\Phi(\cfrac{k-np}{\sqrt{np(1-p)}})$
• $P(X=k)$
  $P(X=k)=P(k-\epsilon < X < k+ \epsilon)$, 再进行如上操作即可

泊松分布

$X \sim P(\lambda)$, $Poisson$

$$P\{X=K\}=\cfrac{\lambda^K}{K!}e^{-\lambda}, k=0, 1, 2, 3..., \lambda >0$$

数学期望为$E(X)=λ$，方差为$D(X)=λ$。

超几何分布

$X \sim H(n, M, N)$, $Hypergeometric$

$$P\{X=K\}=\cfrac{C_{N_1}^{k} C_{N_2}^{n-k}}{C_N^n}, N={N_1+N_2}$$

可用于不放回抽样实验
当N很大，n很小，可视为放回抽样，此时可以使用二项分布计算
$P\{X=K\}=\cfrac{C_{N_1}^{k}C_{N_2}^{n-k}}{C_N^n}\approx C_{n}^{k}p^k(1-p)^{n-k}$

近似计算
超几何分布$\xRightarrow[不放回视为放回]{N大\ \frac{n}{N}小}$二项分布$\xRightarrow[n\ge 100, np \le 10, np=\lambda]{n比较大,p比较小，np适中}$泊松分布

---

连续型

一般具有以下两个重要函数：

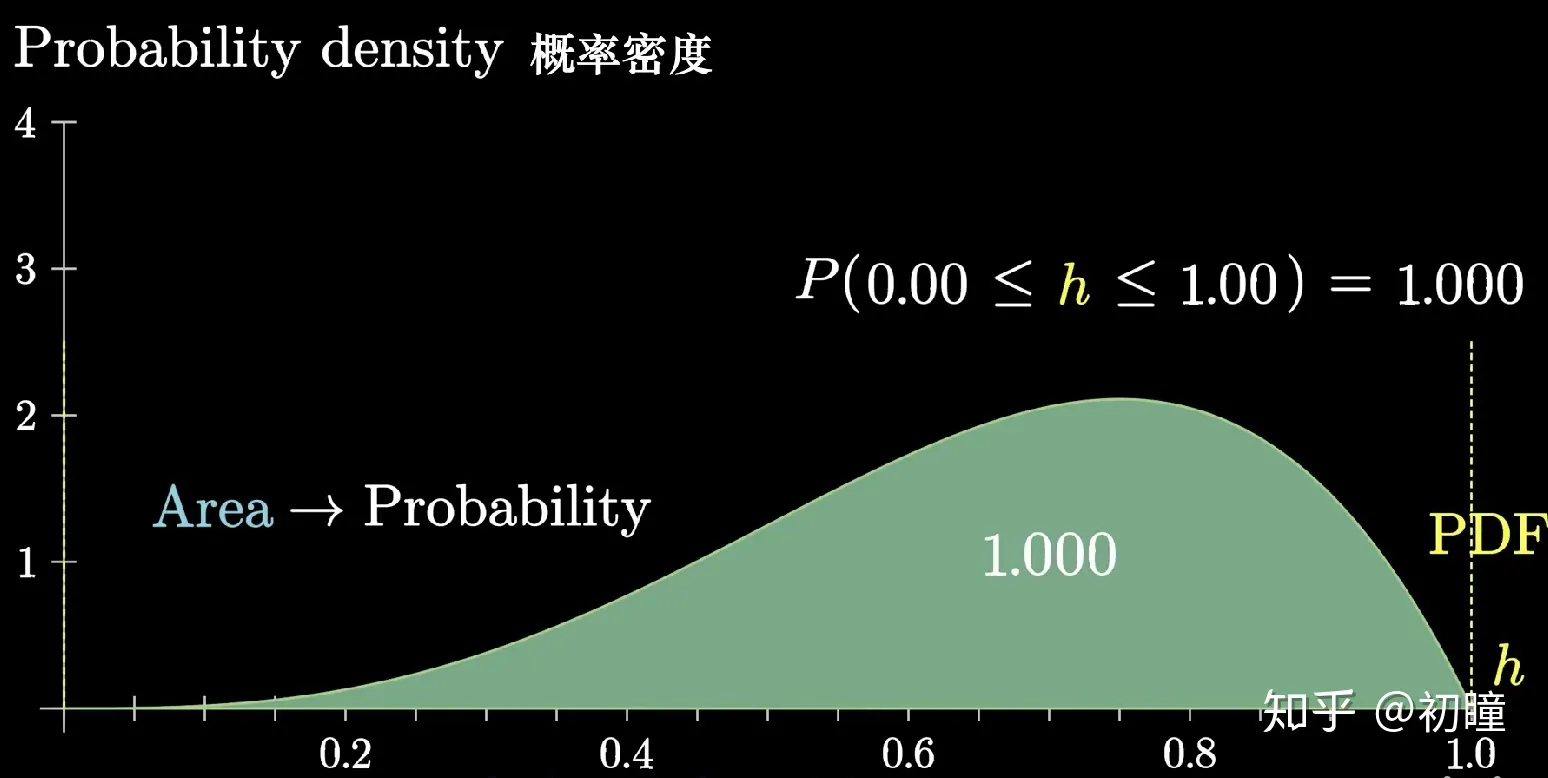
• 概率密度函数$f(x)$

  • 概率密度函数是一个非负的函数，它表示随机变量取某个值或某个区间内的值的可能性大小。概率密度函数的面积就是相应的概率，即
    $P(a≤X≤b)=∫_a^b f(x)dx$
  • 概率密度函数满足以下性质：
    • $f(x)≥0$，对任意x。
    • $\int_{-\infin}^{+\infin} f(x)dx=1$。
    • 如果$P(X=x)=0$，对任意x，则$f(x)$在x处不连续。

• 分布函数$F(x)$

  • 分布函数是一个单调不减的函数，它表示随机变量小于等于某个值的概率。分布函数记为$F(x)=P(X≤x)$
  • 分布函数满足以下性质：
    • $0≤F(x)≤1$，对任意x。
    • $F(-∞)=0$，$F(+∞)=1$。
    • 如果X是连续型随机变量，则$F^\prime(x)=f(x)$，对任意x。

均匀分布

$X \sim U [a, b]$, $uniform$

数学期望为$E(X)=\cfrac{(a+b)}{2}$，方差为$D(X)=\cfrac{(b-a)^2}{12}$

概率密度函数

$$f(x)=\begin{cases} \cfrac{1}{b-a}, & \text{$a\le x \le b$ } \\ 0 & \text{else} \end{cases}$$

分布函数

$$F(x)=\int_{-\infin}^{x} f(t)\,{\rm d}t=\begin{cases} 0 & \text{$x < a$}\\ \cfrac{x-a}{b-a}, & \text{$a\le x \le b$ } \\ 1 & \text{$b<x$} \end{cases}$$

指数分布

$X \sim E_{xp}(\lambda)$, $Exponential$

数学期望为$E(X)=1/λ$，方差为$D(X)=1/λ^2$。

常用于服务时间、寿命

概率密度函数

$$f(x)=\begin{cases} \lambda e^{-\lambda x}, & \text{$x>0$} \\ 0, & \text{$x \le 0$} \end{cases}$$

分布函数

$$F(x)=P\{X\le x\}=\int_{-\infin}^{x} f(t)\,{\rm d}t=\begin{cases} 0, & \text{$x \le 0$} \\ 1-e^{-\lambda x}, & \text{$x>0$} \end{cases}$$

正态分布

$X \sim N (\mu, \sigma^2)$, $Normal$

数学期望为$E(X)=μ$，方差为$D(X)=σ^2$。

又称为高斯分布

一般

概率密度函数

$$\phi (x)=\cfrac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^2}{2 \sigma^2}}, -\infin \le x \le + \infin$$

分布函数

$$\Phi (x)=\cfrac{1}{\sqrt{2 \pi} \sigma} \int_{-\infin}^{x}e^{-\frac{(t-\mu)^2}{2 \sigma^2}}{\rm d} t, -\infin \le x \le + \infin$$

标准

概率密度函数

$$\phi (x)=\cfrac{1}{\sqrt{2 \pi} }e^{-\frac{x^2}{2}}, -\infin \le x \le + \infin$$

分布函数

$$\Phi (x)=\cfrac{1}{\sqrt{2 \pi} } \int_{-\infin}^{x}e^{-\frac{t^2}{2}}{\rm d} t, -\infin \le x \le + \infin$$

数学期望为$E(X)=0$，方差为$D(X)=1$。

抽样分布

正态分布

和前文一致

卡方分布

$Q \sim \chi^2 (v)$

$$f(x)=\cfrac{1}{2^{\frac{n}{2}}\Gamma(\frac{n}{2})}x^{\frac{n}{2}-1}e^{-\frac{x}{2}}, x≥0$$

其中n是自由度，Γ是伽玛函数，数学期望为$E(X)=n$，方差为$D(X)=2n$

是n个相互独立的标准正态分布随机变量的平方和的分布

$$\Sigma_{i-1}^nx_i\sim \chi^2(n), EX=n, DX=2n$$

由中心极限定理，n充分大时，T标准化后

$$\cfrac{T-n}{\sqrt{2n}}\sim N(0, 1), \text{近似计算}$$

t分布

$X \sim t(n)$

若$X\sim N(0, 1)$，$Y\sim \chi^2(n)$，X和Y独立

$$T=\cfrac{X}{\sqrt{\cfrac{Y}{n}}}\sim t(n)$$

n越小，和正态分布差异越大
$n\ge 30$，和正态分布区别很小

上$\alpha$分位数

$P\{T>t_a(n)\}=a$

F分布