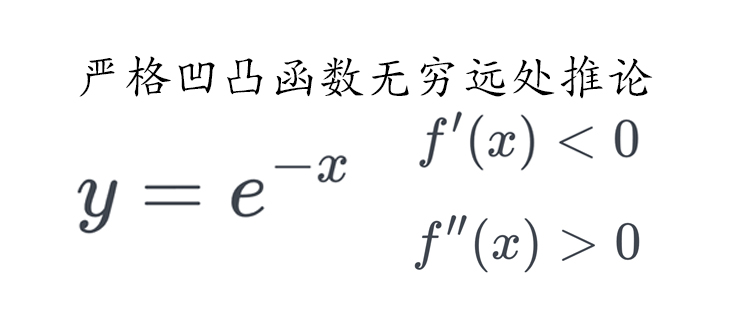高等数学 | 无穷远处趋于零的严格凹凸函数，在无限远处的性质

无穷远处趋于零的严格凹凸函数，在无限远处的性质

问题描述

已知函数 $f(x)$ 满足以下条件：

• $\lim\limits_{x \to +\infty} f(x) = 0$
• $f''(x)$ 在 $\mathbb{R}$ 上恒不为零（即函数有确定的凹凸性）

本文将分类讨论 $f''(x) > 0$（严格凸）和 $f''(x) < 0$（严格凹）两种情况下，以下四个命题的成立情况：

1. $\lim\limits_{x \to +\infty} f'(x) = 0$
2. $f(x)$ 的单调性
3. $f(x)$ 的符号
4. $\lim\limits_{x \to -\infty} f(x)$
5. 级数 $\sum\limits_{n=1}^{\infty} f'(n)$ 的收敛性

---

详细分析

命题1: $\lim\limits_{x \to +\infty} f'(x) = 0$ ✓ 恒成立

证明：
本命题的证明对 $f''(x) > 0$ 和 $f''(x) < 0$ 两种情况完全同构。

• 若 $f''(x) > 0$，则 $f'(x)$ 严格单调递增。
• 若 $f''(x) < 0$，则 $f'(x)$ 严格单调递减。

在两种情况下，$f'(x)$ 均为严格单调函数，因此 $\lim\limits_{x \to +\infty} f'(x)$ 存在（可能为有限值或无穷）。设 $\lim\limits_{x \to +\infty} f'(x) = L$。

情况1： 若 $L > 0$
由极限定义，存在 $x_0 \in \mathbb{R}$，使得当 $x > x_0$ 时，有 $f'(x) > \frac{L}{2} > 0$。
对任意 $x > x_0$，由微积分基本定理：

$$f(x) = f(x_0) + \int_{x_0}^{x} f'(t) \, dt > f(x_0) + \frac{L}{2}(x - x_0)$$

当 $x \to +\infty$ 时，右端趋于 $+\infty$，故 $\lim\limits_{x \to +\infty} f(x) = +\infty$，与已知矛盾。

情况2： 若 $L < 0$
由极限定义，存在 $x_0 \in \mathbb{R}$，使得当 $x > x_0$ 时，有 $f'(x) < \frac{L}{2} < 0$。
对任意 $x > x_0$：

$$f(x) = f(x_0) + \int_{x_0}^{x} f'(t) \, dt < f(x_0) + \frac{L}{2}(x - x_0)$$

当 $x \to +\infty$ 时，右端趋于 $-\infty$，故 $\lim\limits_{x \to +\infty} f(x) = -\infty$，与已知矛盾。

结论： 因此只能 $L = 0$，即 $\lim\limits_{x \to +\infty} f'(x) = 0$。

---

命题2: $f(x)$ 的单调性

该性质依赖于 $f''(x)$ 的符号。

情况一: $f''(x) > 0$ (严格凸) → $f'(x) < 0$ (严格递减)

证明：
已知 $f'(x)$ 严格单调递增，且由命题1知 $\lim\limits_{x \to +\infty} f'(x) = 0$。
一个严格单调递增的函数，其极限为0，那么该函数在整个定义域上的值必定恒小于0。
若存在某点 $x_0$ 使得 $f'(x_0) \geq 0$，则对所有 $x > x_0$，必有 $f'(x) > f'(x_0) \geq 0$，这与 $\lim\limits_{x \to +\infty} f'(x) = 0$ 矛盾。
因此，对所有 $x \in \mathbb{R}$，必有 $f'(x) < 0$，即 $f(x)$ 在 $\mathbb{R}$ 上严格单调递减。

情况二: $f''(x) < 0$ (严格凹) → $f'(x) > 0$ (严格递增)

证明：
已知 $f'(x)$ 严格单调递减，且 $\lim\limits_{x \to +\infty} f'(x) = 0$。
一个严格单调递减的函数，其极限为0，那么该函数在整个定义域上的值必定恒大于0。
若存在某点 $x_0$ 使得 $f'(x_0) \leq 0$，则对所有 $x > x_0$，必有 $f'(x) < f'(x_0) \leq 0$，这与 $\lim\limits_{x \to +\infty} f'(x) = 0$ 矛盾。
因此，对所有 $x \in \mathbb{R}$，必有 $f'(x) > 0$，即 $f(x)$ 在 $\mathbb{R}$ 上严格单调递增。

---

命题3: $f(x)$ 的符号

该性质是命题2的直接推论。

情况一: $f''(x) > 0$ → $f(x) > 0$

证明：
由命题2，$f(x)$ 在 $\mathbb{R}$ 上严格单调递减。结合已知条件 $\lim\limits_{x \to +\infty} f(x) = 0$，可知函数是从上方趋近于0。
对任意 $x_0 \in \mathbb{R}$，由于 $f$ 严格递减，对所有 $x > x_0$ 都有 $f(x_0) > f(x)$。
令 $x \to +\infty$，则 $f(x_0) \geq \lim\limits_{x \to +\infty} f(x) = 0$。
若存在 $f(x_0)=0$，则对所有 $x > x_0$ 都有 $f(x) < 0$，这与 $\lim\limits_{x \to +\infty} f(x) = 0$ 矛盾。
因此对所有 $x \in \mathbb{R}$，必有 $f(x) > 0$。

情况二: $f''(x) < 0$ → $f(x) < 0$

证明：
由命题2，$f(x)$ 在 $\mathbb{R}$ 上严格单调递增。结合已知条件 $\lim\limits_{x \to +\infty} f(x) = 0$，可知函数是从下方趋近于0。
对任意 $x_0 \in \mathbb{R}$，由于 $f$ 严格递增，对所有 $x > x_0$ 都有 $f(x_0) < f(x)$。
令 $x \to +\infty$，则 $f(x_0) \leq \lim\limits_{x \to +\infty} f(x) = 0$。
若存在 $f(x_0)=0$，则对所有 $x > x_0$ 都有 $f(x) > 0$，这与 $\lim\limits_{x \to +\infty} f(x) = 0$ 矛盾。
因此对所有 $x \in \mathbb{R}$，必有 $f(x) < 0$。

---

命题4: $\lim\limits_{x \to -\infty} f(x)$

情况一: $f''(x) > 0$ → $\lim\limits_{x \to -\infty} f(x) = +\infty$

证明：
已知 $f'(x) < 0$ 且严格单调递增。取定 $x_0 \in \mathbb{R}$，对任意 $x < x_0$，由微积分基本定理：

$$f(x) = f(x_0) - \int_{x}^{x_0} f'(t) \, dt = f(x_0) + \int_{x}^{x_0} |f'(t)| \, dt$$

由于 $f'(x)$ 单调递增且恒负，$\lim\limits_{x \to -\infty} f'(x)$ 存在一个负值或为 $-\infty$。在任何一种情况下，积分 $\int_{x}^{x_0} |f'(t)| \, dt$ 当 $x \to -\infty$ 时都趋于 $+\infty$。
因此，$\lim\limits_{x \to -\infty} f(x) = +\infty$。

情况二: $f''(x) < 0$ → $\lim\limits_{x \to -\infty} f(x) = -\infty$

证明：
已知 $f'(x) > 0$ 且严格单调递减。取定 $x_0 \in \mathbb{R}$，对任意 $x < x_0$：

$$f(x) = f(x_0) - \int_{x}^{x_0} f'(t) \, dt$$

由于 $f'(x)$ 单调递减且恒正，$\lim\limits_{x \to -\infty} f'(x)$ 存在一个正值或为 $+\infty$。在任何一种情况下，积分 $\int_{x}^{x_0} f'(t) \, dt$ 当 $x \to -\infty$ 时都趋于 $+\infty$。
因此，$\lim\limits_{x \to -\infty} f(x) = -\infty$。

---

命题5: 级数 $\sum\limits_{n=1}^{\infty} f'(n)$ 的收敛性 ✓ 恒成立

证明：
本命题的证明关键在于利用拉格朗日中值定理，并将级数 $\sum f'(n)$ 与一个可判断敛散性的伸缩级数进行比较。

首先，考虑级数 $\sum\limits_{n=1}^{\infty} [f(n+1) - f(n)]$。其部分和为：

$$S_N = \sum\limits_{n=1}^{N} [f(n+1) - f(n)] = f(N+1) - f(1)$$

由于已知 $\lim\limits_{x \to +\infty} f(x) = 0$，则 $\lim\limits_{N \to \infty} S_N = 0 - f(1) = -f(1)$。
因此，级数 $\sum\limits_{n=1}^{\infty} [f(n+1) - f(n)]$ 收敛。

根据拉格朗日中值定理，对任意 $n \in \mathbb{N}^*$，存在 $\xi_n \in (n, n+1)$，使得：

$$f(n+1) - f(n) = f'(\xi_n)$$

接下来分两种情况讨论：

情况一: $f''(x) > 0$ (严格凸)

此时 $f'(x)$ 严格单调递增且 $f'(x) < 0$。
因此，对于 $\xi_n \in (n, n+1)$，有 $f'(n) < f'(\xi_n) < f'(n+1) < 0$。
结合中值定理，得到 $f'(n) < f(n+1) - f(n) < f'(n+1)$。

我们关心的是级数 $\sum f'(n)$，这是一个负项级数。我们转而研究正项级数 $\sum [-f'(n)]$ 的敛散性。
由上述不等式，两边同乘-1，得：

$$-f'(n) > -[f(n+1) - f(n)] > -f'(n+1) > 0$$

即 $0 < -f'(n+1) < f(n) - f(n+1)$。

考虑正项级数 $\sum\limits_{n=1}^{\infty} [f(n) - f(n+1)]$，其部分和为 $f(1) - f(N+1)$，当 $N \to \infty$ 时极限为 $f(1)$。故该级数收敛。
根据正项级数的比较判别法，由于 $0 < -f'(n+1) < f(n) - f(n+1)$ 且 $\sum [f(n) - f(n+1)]$ 收敛，可知级数 $\sum [-f'(n+1)]$ 收敛，从而 $\sum [-f'(n)]$ 也收敛。
因此，原级数 $\sum\limits_{n=1}^{\infty} f'(n)$ 收敛。

情况二: $f''(x) < 0$ (严格凹)

此时 $f'(x)$ 严格单调递减且 $f'(x) > 0$。
因此，对于 $\xi_n \in (n, n+1)$，有 $f'(n) > f'(\xi_n) > f'(n+1) > 0$。
结合中值定理，得到 $f'(n) > f(n+1) - f(n) > f'(n+1)$。

级数 $\sum f'(n)$ 是一个正项级数。
由不等式 $0 < f'(n+1) < f(n+1) - f(n)$，以及我们已证的级数 $\sum [f(n+1) - f(n)]$ 收敛。
根据正项级数的比较判别法，可知级数 $\sum f'(n+1)$ 收敛，从而 $\sum f'(n)$ 也收敛。

结论： 无论函数是严格凸还是严格凹，级数 $\sum\limits_{n=1}^{\infty} f'(n)$ 都收敛。

---

结论总结

下表总结了在给定条件下，函数由其凹凸性决定的核心性质：

性质推导	$f''(x) > 0$（严格凸）	$f''(x) < 0$（严格凹）
1. 导数极限 $\lim\limits_{x \to +\infty} f'(x)$	$0$	$0$
2. 函数单调性 ($f'(x)$ 符号）	严格递减（$f'(x) < 0$）	严格递增（$f'(x) > 0$）
3. 函数值符号 ($f(x)$ 符号）	恒为正（$f(x) > 0$）	恒为负（$f(x) < 0$）
4. 负无穷极限 $\lim\limits_{x \to -\infty} f(x)$	$+\infty$	$-\infty$
5. 导数级数 $\sum\limits_{n=1}^{\infty} f'(n)$	收敛	收敛

---

几何直观理解

情况一: $f''(x) > 0$ (严格凸)

函数图像是一条开口向上、严格递减的光滑曲线。它从左上方的无穷远处延伸而来，在右侧无限趋近于 $x$ 轴（作为水平渐近线）但永不触及。

• 典型例子： $f(x) = e^{-x}$
  • $f'(x) = -e^{-x} < 0$
  • $f''(x) = e^{-x} > 0$
  • $\lim\limits_{x \to +\infty} e^{-x} = 0$

情况二: $f''(x) < 0$ (严格凹)

函数图像是一条开口向下、严格递增的光滑曲线。它从左下方的无穷远处延伸而来，在右侧无限趋近于 $x$ 轴但永不触及。

• 典型例子： $f(x) = -e^{-x}$
  • $f'(x) = e^{-x} > 0$
  • $f''(x) = -e^{-x} < 0$
  • $\lim\limits_{x \to +\infty} -e^{-x} = 0$

---

关键推理链

本题的证明形成了两条平行的、由凹凸性决定的逻辑链：

f''(x) > 0 (凸)             f''(x) < 0 (凹)
    │                           │
    ▼                           ▼
f'(x) 严格递增                f'(x) 严格递减
    │                           │
    └─────────┐   ┌─────────────┘
              │   │
              ▼   ▼
     lim_{x→+∞} f(x) = 0
                │
                ▼
    lim_{x→+∞} f'(x) = 0  (共同结论)
                │
    ┌───────────┴────────────────┐
    ▼                            ▼
f'(x) < 0 (递减)            f'(x) > 0 (递增)
    │                            │
    ▼                            ▼
f(x) > 0 (值恒正)           f(x) < 0 (值恒负)
    │                            │
    ▼                            ▼
lim_{x→-∞}f(x)=+∞           lim_{x→-∞}f(x)=-∞
    │                            │
    ▼                            ▼
  Σf'(n) 收敛                Σf'(n) 收敛

核心洞察： 函数在无穷远处的极限行为，结合其全局的凹凸性，几乎完全决定了函数导数、函数值以及另一端极限的性质。初始条件的微小改变（二阶导数符号反转）会导致后续推论的系统性反转。而导数形成的级数 $\sum f'(n)$ 的收敛性则是一个更深层次的、不受凹凸性影响的共同特征。

函数图像示例

情况一 ($f''(x) > 0$) 的典型图像：

若改为：