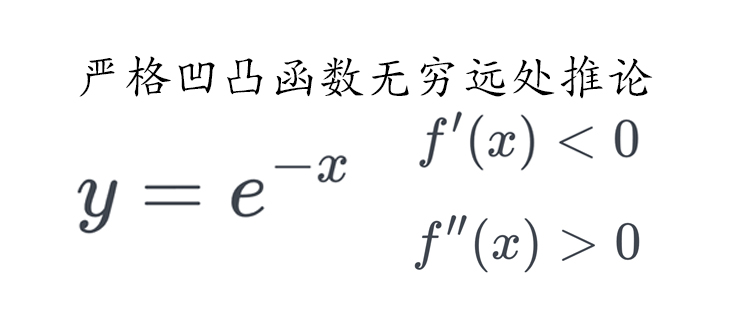高等数学 | 二元函数极值、海赛矩阵与李亚普诺夫稳定性分析
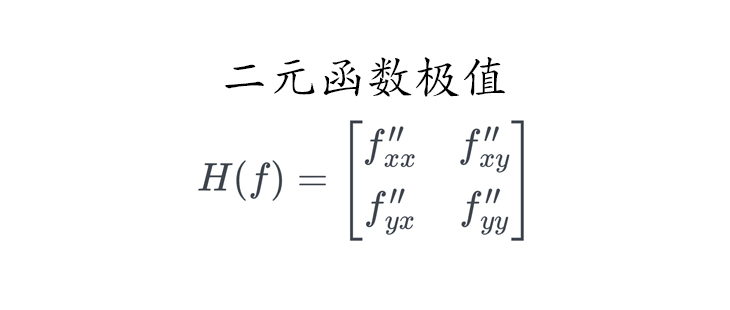
高等数学 | 二元函数极值、海赛矩阵与李亚普诺夫稳定性分析
Prong二元函数极值、海赛矩阵与李亚普诺夫稳定性分析——从一元到二元的推广
一元函数极值与拐点回顾
在分析更复杂的二元函数之前,我们首先回顾一下一元函数中两个核心概念:极值点和拐点的判定法则。这有助于我们理解这些思想如何被推广到更高维度。
1. 极值点 (Local Extrema)
极值点是函数曲线上局部的“山峰”(极大值)或“山谷”(极小值)。
-
必要条件:若函数 在点 可导且取得极值,则其一阶导数必为零,即 。因此,极值的候选点(也称驻点或临界点)是满足 或导数不存在的点。
-
第一充分条件 (一阶导数左右变号):设函数在 连续,在 的去心邻域可导。
- 若在 左侧 而右侧 ,则 为极大值。
- 若在 左侧 而右侧 ,则 为极小值。
- 若 在 两侧符号不变,则不是极值点。
-
第二充分条件 (一阶导数为零,二阶导数不为零):设 且 存在。
- 若 ,则 为极大值。
- 若 ,则 为极小值。
-
第 n 阶导数检验法(奇数阶导数为零,偶数阶导数不为零):若 ,但 :
- 当 n 为偶数时,若 ,则为极大值;若 ,则为极小值。
- 当 n 为奇数时, 不是极值点。
核心思想:为何高阶导数如此重要?
当 时,二阶导数检验法会失效。这背后的直观解释是,函数在 点附近的变化极其平坦,以至于标准的二次近似(像抛物线)已经无法捕捉其真实的弯曲行为。例如函数 ,它在 点比任何抛物线都“平”,因此其二阶导数为零。我们必须借助更高阶的导数(在此例中是四阶导数)才能“看透”这种平坦,发现其依然构成了一个极小值。
2. 拐点 (Inflection Point)
拐点是函数曲线凹凸性发生改变的点,即曲线从“向上凹”变为“向下凹”或反之。
-
必要条件:若 是拐点且 存在,则 。因此,拐点的候选点是满足 或二阶导数不存在的点。
-
第一充分条件 (二阶导数变号):若 在 两侧异号,则 是拐点。
-
第二充分条件 (二阶导数为零,三阶导数不为零):设 且 ,则 是拐点。
-
第 n 阶导数检验法(偶数阶导数为零,奇数阶导数不为零):若 ,但 :
- 当 n 为奇数 () 时, 是拐点。
核心思想:同理
与极值点类似,当 时,三阶导数检验法也会失效。例如函数 ,它在 点的变化同样非常平坦,需要通过五阶导数才能确定其拐点性质。
现在,我们将这些思想从一元函数推广到二元函数。
二元函数极值问题陈述
一个二元函数 $ f(x, y) $ 具有二阶连续偏导数,并在点 $ P_0(x_0, y_0) $ 取得极大值。
我们需要回答以下三个问题:
- 在点 $ P_0 f_{xx}‘’$ 和 的符号是什么(大于零还是小于零)?
- 这和海赛(Hessian)矩阵有什么关系?
- 这和李亚普诺夫(Lyapunov)稳定性定理有什么关系?
核心问题回答
对于一个在 $ P_0 $ 点取极大值的二元函数,其二阶偏导数满足:
等于0也可能取极值,这一点在后面会讨论。
下面,我们将通过三种不同的方法来分析和解释这个结论。
方法一:常规方法(二阶偏导数检验法)
这是微积分中最标准的判断二元函数极值的方法。
1. 必要条件
函数在某点取得极值的必要条件是该点为驻点(Critical Point),即它的一阶偏导数(梯度)为零。
2. 充分条件
为了判断驻点是极大值、极小值还是鞍点,我们需要使用二阶偏导数。记:
并定义判别式:
根据二阶偏导数检验法:
- 如果 $ \Delta > 0 $ 且 $ A < 0 $,则 $ f(P_0) $ 是一个局部极大值。
- 如果 $ \Delta > 0 $ 且 $ A > 0 $,则 $ f(P_0) $ 是一个局部极小值。
- 如果 $ \Delta < 0 $,则 $ P_0 $ 是一个鞍点。
- 如果 $ \Delta = 0 $,则此方法失效,需要更高阶的检验。
4. 检验法失效的情况:与一元函数的类比
我们来探讨当 时会发生什么,特别是当 且 的情况。
此时,判别式
- 若 ,则 ,该点明确为鞍点。
- 若 ,则 ,二阶检验法完全失效。
这个失效的情况,与一元函数中 的情况是完全对应的。它意味着函数的局部形状过于平坦,无法用一个二次曲面来近似。此时,我们必须通过其他方法来判断。
示例:
这是一个经典例子,它是一元函数 在二维空间的直接推广。
- 驻点:,解得驻点为 。
- 二阶导数:, , 。
- 在驻点 :, , 。
- 判别式:。检验法失效。
然而,通过直接分析函数可知,。对于任何不为 的点,都有 。因此, 点是一个局部极小值点。这个例子清晰地表明,即使二阶偏导数全为零,函数仍然可能取得极值。
3. 结论推导
根据题目,$ P_0 $ 是极大值点,因此必须满足 $ \Delta > 0 $ 且 $ A < 0 $。
即:
- $ A = f_{xx}‘’(P_0) < 0 $
-
从条件2可以推导出
由于 ,所以 $ f_{xx}‘’(P_0) $ 和 $ f_{yy}‘’(P_0) $ 必须同号。
又因为条件1告诉我们 $ f_{xx}‘’(P_0) < 0 $,所以 $ f_{yy}‘’(P_0) $ 也必须小于零。
因此,通过常规方法,我们证明了在极大值点 $ P_0 f_{xx}‘’ < 0$ 且 。
方法二:海赛矩阵(Hessian Matrix)法
海赛矩阵提供了一种更系统、更优雅的方式来表达二阶导数检验,并且可以轻松推广到更高维的函数。
1. 海赛矩阵的定义
对于二元函数 $ f(x, y) $,其海赛矩阵是一个 $ 2 \times 2 $ 的对称矩阵,由所有二阶偏导数构成:
由于函数具有二阶连续偏导数,根据克莱罗定理,$ f_{xy}‘’ = f_{yx}‘’ $。
2. 海赛矩阵与函数极值
函数在驻点 $ P_0 $ 附近的性态由海赛矩阵 $ H(P_0) $ 的定正性决定。
- 如果 $ H(P_0) $ 是正定的,则 $ f(P_0) $ 是局部极小值。
- 如果 $ H(P_0) $ 是负定的,则 $ f(P_0) $ 是局部极大值。
- 如果 $ H(P_0) $ 是不定的(有正有负的特征值),则 $ P_0 $ 是鞍点。
3. 负定矩阵的判定
一个对称矩阵是负定的,当且仅当它的所有顺序主子式(leading principal minors)符号交错,并以负号开头。
对于 $ 2 \times 2 $ 的海赛矩阵 $ H(P_0) $:
- 一阶顺序主子式:$ D_1 = f_{xx}‘’(P_0) $
- 二阶顺序主子式:$$
\begin{aligned}
D_2 = \det(H(P_0)) = f_{xx}‘’(P_0)f_{yy}‘’(P_0) - (f_{xy}‘’(P_0))^2
\end{aligned}
这组条件与方法一中 $ A < 0 $ 和 $ \Delta > 0 $ 是完全等价的。因此,海赛矩阵方法同样导出了 $ f_{xx}‘’ < 0 $ 和 $ f_{yy}‘’ < 0 $ 的结论。海赛矩阵提供了一个更深刻的代数视角,将极值问题与矩阵的性质联系在了一起。
方法三:与李亚普诺夫(Lyapunov)定理的联系
李亚普诺夫稳定性理论是研究动态系统(如微分方程)平衡点稳定性的核心工具。虽然函数求极值是一个静态问题,但我们可以通过构造一个动态系统来建立两者之间的联系。
1. 构造动态系统
我们可以将寻找函数 $ f(x, y) $ 极值的过程看作一个“寻山”或“寻谷”的过程。考虑一个梯度上升系统,其运动方向始终沿着函数值增长最快的方向(梯度方向):
这个系统的平衡点(Equilibrium Points)正是 $ \nabla f(\mathbf{x}) = \mathbf{0} $ 的点,即 $ f(x, y) $ 的驻点。
- 系统的稳定平衡点对应于 $ f(x, y) $ 的极大值(所有路径最终都会汇集到山顶)。
- 系统的不稳定平衡点对应于 $ f(x, y) $ 的极小值或鞍点(从山谷或山脊的最高点出发,稍有扰动就会离开)。
2. 李亚普诺夫第一法(线性化方法)
该方法通过分析系统在平衡点 $ \mathbf{x}_0 $(即驻点 $ P_0 $)附近的线性化行为来判断其稳定性。线性化系统的矩阵(雅可比矩阵)为:
我们发现,这个梯度系统的雅可比矩阵正是函数 $ f $ 的海赛矩阵。
3. 李亚普诺夫稳定性定理
李亚普诺夫稳定性定理指出:
- 如果雅可比矩阵 $ J(\mathbf{x}_0) $ 的所有特征值的实部都为负,则平衡点 $ \mathbf{x}_0 $ 是渐进稳定的。
- 如果至少有一个特征值的实部为正,则平衡点是不稳定的。
3. 结论推导
由于 $ P_0 $ 是极大值点,它对应于我们构造的梯度上升系统的稳定平衡点。因此,其雅可比矩阵(即海赛矩阵 $ H(P_0) $)的所有特征值的实部必须为负。
因为 $ H(P_0) $ 是一个实对称矩阵,它的特征值都是实数。所以,条件简化为:$ H(P_0) $ 的所有特征值都必须是负数。
一个矩阵的所有特征值都为负,这正是该矩阵是负定矩阵的定义之一。
对于一个 $ 2 \times 2 $ 矩阵,其特征值 $ \lambda_1, \lambda_2 $ 满足:
要使 $ \lambda_1, \lambda_2 $ 均为负数,必须满足:
这组条件与海赛矩阵负定的条件是等价的,并且同样能推导出 $ f_{xx}‘’ < 0 $ 和 $ f_{yy}‘’ < 0 $。
总结
三种方法从不同角度得到了相同的结论。在二元函数 $ f(x, y) $ 的极大值点 $ P_0 $:
- 直接结论:$ f_{xx}‘’(P_0) < 0 $ 且 $ f_{yy}‘’(P_0) < 0 $。这在几何上意味着函数曲面在 $ P_0 $ 点沿着坐标轴方向都是“向下凹”的。
- 与海赛矩阵的关系:条件等价于海赛矩阵 $ H(P_0) $ 是负定的。这是对局部曲率更完整、更本质的代数描述。
- 与李亚普诺夫定理的关系:通过构造一个梯度上升动态系统,函数的极大值点对应于系统的稳定平衡点。利用李亚普诺夫线性化方法,平衡点的稳定性条件最终归结为其雅可比矩阵(即海赛矩阵)的负定性。这巧妙地将静态优化问题与动态系统稳定性理论联系在了一起。
附录:什么是鞍点(Saddle Point)?
简单来说,鞍点(Saddle Point) 是函数的一个驻点(也就是梯度为零的点),但它既不是局部极大值也不是局部极小值。
1. 直观理解:马鞍的形状
想象一个马鞍:
- 沿着马背的方向(前后方向),马鞍是向上弯曲的,这个方向的最低点就是鞍点。
- 沿着骑手大腿的方向(左右方向),马鞍是向下弯曲的,这个方向的最高点也是同一个鞍点。
因此,在一个方向上看,这个点像是极小值;但在另一个方向上看,它又像是极大值。这种在一个方向上“凹”而在另一个方向上“凸”的驻点,就是鞍点。任何微小的移动,都可能让函数值上升或下降,这取决于你移动的方向。
2. 数学上的判断
对于一个二元函数 $ f(x, y) $,一个点 $ P_0 $ 是鞍点的充分条件是:
- 该点是一阶导数为零的驻点:$ \nabla f(P_0) = (0, 0) $。
- 其海赛矩阵的判别式小于零:$$ \Delta = f_{xx}‘‘f_{yy}’’ - (f_{xy}‘’)^2 < 0 $$
这个条件意味着海赛矩阵是不定的,它有一个正特征值和一个负特征值,分别对应了函数曲面在该点一个方向向上弯曲,一个方向向下弯曲。